421.数组中两个数的最大异或值

发表于 更新于 分类于 阅读次数： 本文字数： 1k 阅读时长 ≈ 1 分钟

题目描述

给你一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 0 ≤ i ≤ j < n 。 - 要求在O(n)时间内解决这个问题 - 限制：1 <= nums.length <= 2 * 10^4 0 <= nums[i] <= 2^31 - 1

题解

异或运算的真值表如下 (相同为0，不同为1)，又称为不进位加法：

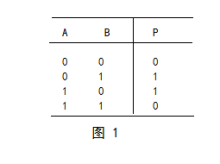图

要找到最大的数，我们要尽量选择高位异或结果为“1”的，所以我们可以将nums中的数加入一个Trie中，然后每次贪心的进行匹配，找到可以使得当前位为1的节点。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {

    class Node {
        Node[] node = new Node[2];
    }

    Node node = new Node();

    void add(int x) {
        Node p = node;
        for (int i = 31; i >= 0; i--) {
            int u = (x >> i) & 1;
            if (p.node[u] == null) p.node[u] = new Node(); 
            p = p.node[u];
        }
    }

    int getVal(int x) {
        int ans = 0;
        Node p = node;
        for (int i = 31; i >= 0; i--) {
            int a = (x >> i) & 1, b = 1 - a;
            if (p.node[b] != null) {
                ans |= (b << i);
                p = p.node[b];
            } else {
                ans |= (a << i);
                p = p.node[a];
            }
        }
        return ans;
    }

    public int findMaximumXOR(int[] nums) {
        int ans = 0;
        for (int i : nums) {
            add(i);
            int j = getVal(i);
            ans = Math.max(ans, i ^ j);
        }
        return ans;
    }
}

参考资料

【宫水三叶の相信科学系列】详解为何能用「贪心」&「Trie」找「最大异或结果」 - 数组中两个数的最大异或值 - 力扣（LeetCode） (leetcode-cn.com)