算法：回溯法学习记录

回溯法是一种非常常见的算法，八皇后问题和迷宫问题都可以使用回溯法进行求解。以下是百度百科中对于回溯法的解释

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。 ——百度百科

回溯法采用一种试探回溯的思想。我们从一个一个分支逐步深入，一旦发现当前分支不是我们所需要的，就排除当前分支，然后回到上一步试探其他分支。迷宫问题就是一种常见的使用回溯法的算法问题。事实上，在现实生活中走迷宫我们也经常使用这种试探的走法。

除了迷宫问题，全排列问题，八皇后问题也都是回溯法的典型问题

八皇后问题

问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

对于八皇后问题，我们采用逐行试探的方法。先在当前行找到一个符合条件的位置放置皇后，如果找不到，就回溯一行排除当前位置继续寻找，直到在最后一行找到一个合适的位置，就可以得到一个解。

一下是四皇后问题的一个解的寻找过程。首先在(0,0)处放置皇后，转移到行1，查找到第一个合法的位置为(1,3)。

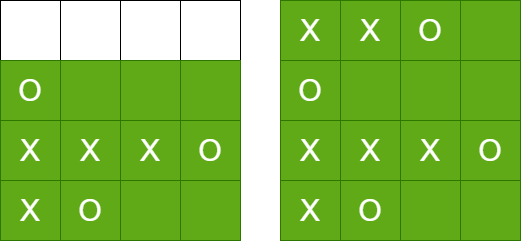
接着搜寻行2，发现没有符合条件的位置，于是回溯到行1，继续寻找下一个合法的位置(1,4)。

继续试探到行2，找到了一个合法的位置(2,1)。

发现在这种情况下行3没有合法的位置，回溯到行2，发现行2剩余的位置也没有合法的，回溯到行1，行1已经没有剩余位置，直接回溯到第0行。

接着试探，起始位置为(0,1)。第1行试探，皇后放在(1,3)

第2行，皇后放在(2,0)。第3行，皇后放在(3,2)。四皇后问题的第一个解找到。

代码实现中特别需要关注的问题是循环何时终止，以及对于边界的处理。

# include <stdio.h>
# include <stdbool.h>
# define QUEENS 4
# define EMPTY 0
# define FULL 1


int checkboard[QUEENS][QUEENS] = { 0 };
int boardrow[QUEENS] = { 0 };

// 只需要判断当前行与之前几行是否冲突
// assert： 0<=x<QUEENS && 0<=y<QUEENS
bool collide(int x, int y) {
    int i = x - 1, j = y - 1, k = y + 1;
    while (i >= 0 && (j >= 0 || k < QUEENS)) {
        if (checkboard[i][y] == FULL)
            return true;
        if (j >= 0 && checkboard[i][j--] == FULL)
            return true;
        if (k < QUEENS && checkboard[i][k++] == FULL)
            return true;
        i--;
    }
    return false;
}

void drawBoard() {
    printf("---------------\n");
    for (int i = 0; i < QUEENS; i++) {
        for (int j = 0; j < QUEENS; j++) {
            printf("%d | ", checkboard[i][j]);
        }
        printf("\n---------------\n");
    }
    printf("\n");
}


// 注意边界状态
// 注意循环结束判断
int Queen() {
    int x = 0, y = 0; // 棋盘坐标
    int numOfSol = 0;
    while (x >= 0 || y < QUEENS) {
        /* 何时回溯
         * 1. 当前行数达到最大（得到一个解）
         * 2. 列数达到最大（当前情况解已经列举完毕）
         */
        if (x >= QUEENS) {
            numOfSol++;
            x--;
            drawBoard();
            y = boardrow[x];
            checkboard[x][y++] = EMPTY;
        }
        else if (y >= QUEENS) {
            x--;
            if (x < 0) break;
            y = boardrow[x];
            checkboard[x][y++] = EMPTY;
        }
        else if (collide(x, y)) {
            // 如果冲突，移动至当前行下一列
            y++;
        }
        else {
            // 如果不冲突，并且在范围内
            // 那么移动至下一行首列
            checkboard[x][y] = FULL;
            boardrow[x++] = y;
            y = 0;
        }
    }
    return numOfSol;
}

int main() {
    int c = Queen();
    printf("Number of Solution: %d", c);
}

这里循环结束的终点条件是当回溯到第0行第4列时，就会继续回溯到第-1行，也就是x<0时结束整个循环。