图形学入门笔记1: 图形学中的数学
数学在图形学中是非常重要的基础,本篇简要记录一下图形学之中的一些数学基础和技巧
线性代数基础
线代在图形学中是非常重要的数学。在图形学中,一些基础的线性代数知识是必须要掌握的,比如向量与矩阵的相关运算
- Vector Addition, Scalar Multiplication, Scalar Product, Normalization, Cross Product
- Vector Cross Product: \(V_1\times V_2=u|V_1||V_2|\sin\theta=\left|\begin{matrix}u_x & u_y & u_z \\ v_{1x} & v_{1y} & v_{1z} \\ v_{2x} & v_{2y} & v_{2z} \end{matrix}\right|\)
- Vector Cross product properties: 1. \(V_1 \times V_2 = -(V_2 \times V_1)\) (不符合交换律) 2. \(V_1 \times (V_2 \times V_3) \neq (V_1 \times V_2) \times V_3\) (不符合交换律) 3. \(V_1 \times (V_2 + V_3)=V_1 \times V_2 + V_1 \times V_3\) (符合结合律)
- Matrix-matrix multiplication, Matrix-vector multiplication
二维三维变换与齐次坐标系
利用线性代数中的向量和矩阵,我们可以表示出在二维平面和三维空间中点线面的位置与相应的关系。首先,我们需要引入齐次坐标的概念,为了简便,以下都以三维空间中的齐次坐标为例。普通的三维坐标表示为\((x,y,z)\),但是在齐次坐标系中,我们添加一个维度\(w\)用来标明该坐标为向量还是坐标,如果是空间中的点就是1,如果是向量就是0,并且齐次坐标满足以下规则,\((x,y,z,w)=(x/w,y/w,z/w,1)\),即原坐标与每个维度乘以相同的数之后得到的坐标是等价的。通过齐次坐标系,我们就可以得到常见的基本变换的矩阵表示。
平移 (Translation) \[ \text{Translation: }\left( \begin{matrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{matrix} \right) \text{, Inverse: } \left( \begin{matrix} 1 & 0 & 0 & -T_x \\ 0 & 1 & 0 & -T_y \\ 0 & 0 & 1 & -T_z \\ 0 & 0 & 0 & 1 \end{matrix} \right) \]
缩放 (Scaling) \[ \text{Scaling:} \left( \begin{matrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right) \]
旋转 (Rotation) 逆时针 \[ R_x(\alpha)= \left( \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos{\alpha} & -\sin{\alpha} & 0 \\ 0 & \sin{\alpha} & \cos{\alpha} & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right), R_y(\alpha)= \left( \begin{matrix} \cos{\alpha} & 0 & \sin{\alpha} & 0 \\ 0 & 1 & 0 & 0 \\ -\sin{\alpha} & 0 & \cos{\alpha} & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right), R_z(\alpha)= \left( \begin{matrix} \cos{\alpha} & -\sin{\alpha} & 0 & 0 \\ \sin{\alpha} & \cos{\alpha} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right), \] 绕着轴\(n\)旋转角度\(\alpha\) (Rodrigues' Rotation Formula) \[ R(n,\alpha)=\cos(\alpha)\mathbf{I}+(1-\cos(\alpha))\mathbf{nn^T}+\sin(\alpha) \underbrace{ \left( \begin{matrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{matrix} \right)} \] 欧拉角:\(R_{xyz}(\alpha, \beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)\):
桶滚 (roll), 偏航 (yaw), 俯仰 (pitch)
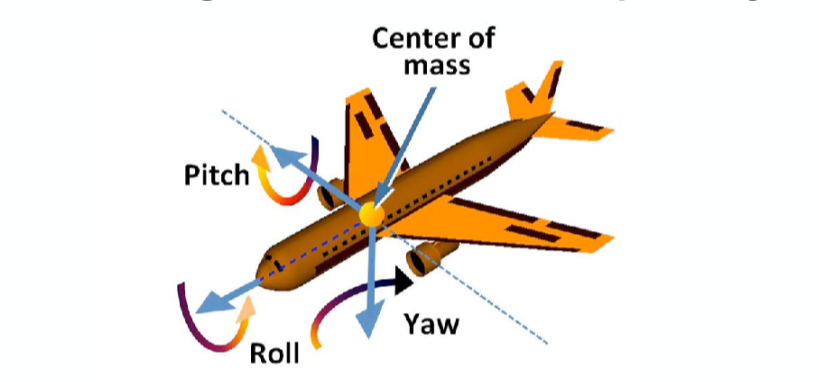
补充: 旋转除了使用坐标进行计算之外,还可以使用四元数进行计算,四元数这里推荐两个YouTube视频
二维与三维几何的基础知识
二维几何知识
计算点到直线距离 [\(A(x_1,y_1),B(x_2,y_2),P(x,y)\)]
- 直线方向向量:\(\vec{v}=(x_2-x_1, y_2-y_1)=(d_x,d_y)\)
- 直线的法线向量 (垂直于直线):\(\vec{n}=(-d_y,d_x)=(y_1-y_2,x_2-x_1)\)
- \(\vec{n},\vec{v}\)转化为单位向量 (Normalization)
- 向量点乘找到距离: \(h=|(P-A)\cdot \hat{n}|\)
两条直线相交(非常简单),联立方程解出交点即可
给定一个点\(P\)和一条直线\(AB\),判断点在直线的哪一侧
使用三角形的有向面积 (Signed area) \(\gamma=\frac{1}{2}Det\left|\begin{matrix}x_a & x_b & x \\ y_a & y_b & y \\ 1 & 1 & 1\end{matrix}\right|, \begin{cases}\gamma>0,left\\\gamma<0,right\\\gamma=0,on\space line\end{cases}\)
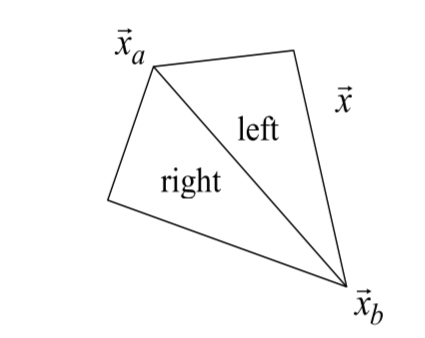
多边形的有向面积:\(polygon\space area=\frac{1}{2}\sum{Det\left|\begin{matrix}x_i & x_{i+1} \\ y_i & y_{i+1}\end{matrix}\right|}\) (Note: 不能忘记最后一个点和第一个点)
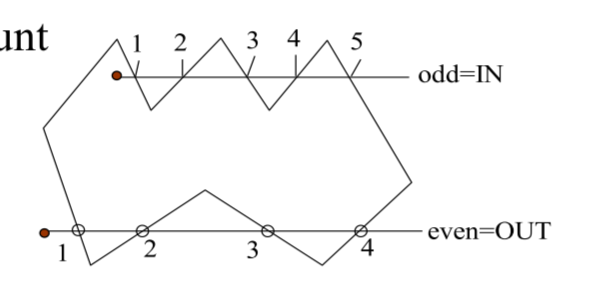
判断点是否在多边形内部1
法一:使用(3)的方法判断点在多边形的每一条边的哪一侧,进而判断点是否在多边形的内部
法二:如果一个点在多边形内部,过这个点任意做一条直线,与多边形的边的交点个数为奇数,如果为偶数,说明这个点在多边形的外部 (注意:还有一些特殊情况需要考虑)
三维几何知识
线性差值 (Linear Interpolation) [Lerp]: \(V=V_0+t(V_1-V_0)\) (点\(V\)在\(V_0\)和\(V_1\)的直线上移动 )
质心坐标 (Barycentric coordinate)
\(P=\alpha P_0+\beta P_1 + \gamma P_2 \text{ where } \alpha+\beta+\gamma=1,A_0=\alpha A, A_1=\beta A,A_2=\gamma A\)
球面线性差值 (Spherical Linear Interpolation) [Slerp]
\(\vec{V(t)}=\vec{V_0}\frac{\sin((1-t)\theta)}{\sin\theta}+\vec{V_1}\frac{\sin(t\theta)}{\sin\theta}\) (\(V\)在\(V_0\)和\(V_1\)之间的弧线上移动 )
三角形的法线,假设三角形三个顶点\(V_0,V_1,V_2\),将两条边按照逆时针方向进行叉乘,得到的结果就是三角形的法线 \[ \vec{n}=(V_1-V_0)\times(V_2-V_0) \text{ OR } (V_1-V_1) \cdots \]
顶点的法线: 取周围多个面的法线的平均值
本篇笔记基于上课的课件以及Games101进行整理