Latex的使用详解笔记(常用数学符号、图片表格等)持续更新

本篇笔记用来记录在使用LaTeX过程中经常碰到的LaTeX数学符号以及一些基础的常用的操作比如添加图片，添加代码，如果有的话还会收藏一些比较实用的模板比如CV模板，作业模板论文模板等等。持续更新……

\(\LaTeX\) 数学

为了使用 AMS-LaTeX 提供的数学功能，我们需要在导言区加载 amsmath 宏包：

\usepackage{amsmath}

LaTeX 的数学模式有两种：行内模式 (inline) 和行间模式 (display)。前者在正文的行文中，插入数学公式；后者独立排列单独成行，并自动居中。

在行文中，使用$ ... $ 可以插入行内公式，使用 \[ ... \] 可以插入行间公式，如果需要对行间公式进行编号，则可以使用 equation 环境：

\begin{equation}
...
\end{equation}

一些比较常用的特殊符号整理

• 各类希腊字母编辑表

  α	β	ω	\(\Theta\)	\(\Gamma\)	\(\Omega\)

• 上下标

  ​ 上标： ^ 如 \(x^2\) ​ 下标： _ 如 \(x_2\) ​ 上下标如果多于一个字母或符号,需要用一对 {} 括起来。

• 根号： 如$sqrt[n]{5}为\(\sqrt[n]5\)

• 省略号：$\dots \cdots$分别为\(\dots \cdots\)

• 运算符 小的运算符(operator)例如 + - * /等可以直接输入，其他特殊的有

  ±	×	÷	⋅	∩	∪	≥	≤	≠	≈	≡

  求和：\sum_1^n: \(\sum_1^n\) 积分：\int_1^n: \(\int_1^n\) 极限：lim_{x \to \infty}: \(lim_{x \to \infty}\) 分数的表示：\frac{}{}如 \(\frac{3}{8}\)

• 字母的特殊标记

  平均数: \overline{mean} or \bar x: \(\overline{mean} \text{ or } \bar m\)

  Hat: \hat{\theta}: \(\hat{\theta}\)

• 矩阵与行列式 $$\begin{matrix}…\end{matrix}$$，使用&分隔同行元素，。如：

  $$
  \begin{matrix}
      1 & x & x^2 \\
      1 & y & y^2 \\
      1 & z & z^2 \\
      \end{matrix}
  $$

  \[ \begin{matrix} 1 & x & x^2 \\\\ 1 & y & y^2 \\\\ 1 & z & z^2 \\\\ \end{matrix} \] 行列式

  $$
  X=\left|
      \begin{matrix}
          x_{11} & x_{12} & \cdots & x_{1d}\\
          x_{21} & x_{22} & \cdots & x_{2d}\\
          \vdots & \vdots & \ddots & \vdots\\
          x_{m1} & x_{m2} & \cdots & x_{md}\\
      \end{matrix}
  \right|
  $$

  \[ X=\left| \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d}\\\\ x_{21} & x_{22} & \cdots & x_{2d}\\\\ \vdots & \vdots & \ddots & \vdots\\\\ x_{m1} & x_{m2} & \cdots & x_{md}\\\\ \end{matrix} \right| \]

• 分隔符 各种括号用 () [] {} \langle \rangle (\(\langle\rangle\))等命令表示,注意花括号通常用来输入命令和环境的参数,所以在数学公式中它们前面要加 \。可以在上述分隔符前面加 \big \Big \bigg \Bigg 等命令来调整大小。

• 方程

  \begin{equation}
  E=mc^2
  \end{equation}

  \[ \begin{equation} E=mc^2 \end{equation} \]

• 分段函数

  f(n) =
  \begin{cases}
  n/2,  & \text{if $n$ is even} \\
  3n+1, & \text{if $n$ is odd}
  \end{cases}

  \[ f(n) = \begin{cases} n/2, & \text{if $n$ is even} \\\\ 3n+1, & \text{if $n$ is odd} \end{cases} \]

• 方程组

  \left\{ 
  \begin{array}{c}
      a_1x+b_1y+c_1z=d_1 \\ 
      a_2x+b_2y+c_2z=d_2 \\ 
      a_3x+b_3y+c_3z=d_3
  \end{array}
  \right

  \[ \left\{ \begin{array}{c} a_1x+b_1y+c_1z=d_1 \\\\ a_2x+b_2y+c_2z=d_2 \\\\ a_3x+b_3y+c_3z=d_3 \end{array} \right. \]

常用公式

• 线性模型

  h(\theta) = \sum_{j = 0} ^n \theta_j x_j

  \[ h(\theta) = \sum_{j = 0} ^n \theta_j x_j \]

• 均方误差

  $$
  J(\theta) = \frac{1}{2m}\sum_{i = 0} ^m(y^i - h_\theta (x^i))^2
  $$

  \[ J(\theta) = \frac{1}{2m}\sum_{i = 0} ^m(y^i - h_\theta (x^i))^2 \]

• 批量梯度下降

  $$
  \frac{\partial J(\theta)}{\partial\theta_j}=\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j
  $$

  \[ \frac{\partial J(\theta)}{\partial\theta_j}=-\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j \]

• 推导过程：

  $$
  \begin{align}
  \frac{\partial J(\theta)}{\partial\theta_j}
  & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i)) \\
  & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_jx_j^i-y^i) \\
  & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j
  \end{align}
  $$

  \[ \begin{align} \frac{\partial J(\theta)}{\partial\theta_j} & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i)) \\\\ & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_jx_j^i-y^i) \\\\ & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j \end{align} \]

• 组合数：\(\tbinom{n}{m}\)$\tbinom{n}{m}$ 或者 \(C^m_n\)

• 线性回归的解析解 \[ \begin{align} \theta_1 &= \frac{\sum_{i=1}^m{(x^{(i)}-\bar{x})(y^{(i)}-\bar{y})}}{\sum^m_{i=1}{(x^{(i)}-\bar{x})^2}} \\ \theta_0 &= \bar{y}-\theta_1\bar{x} \end{align} \]

  \[ \hat{\Theta}=\Theta^*=(\mathbf{X}^T\mathbf{X})^{-1}X^TY \]

参考资料

1. 一份其实很短的 LaTeX 入门文档

2. 试试LaTeX插入数学公式

3. 在博客中使用LaTeX插入数学公式

4. MathJax basic tutorial and quick reference

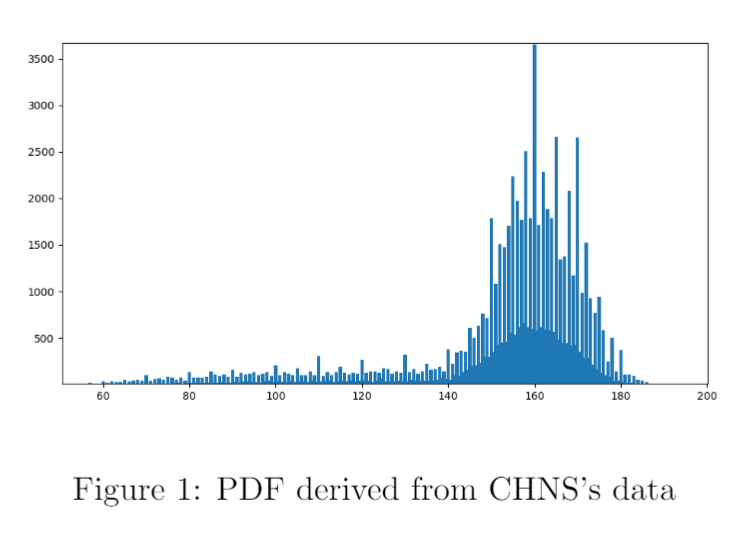
在\(\LaTeX\)中插入图片

单张图片插入

\begin{figure}[H]
    \centering										% 设置居中
    \includegraphics[width=10cm]{fig/Figure_2.png}	% 图片路径和大小设置
    \caption{PDF derived from CHNS's data }			% 图片下文字(caption)
\end{figure}

[注]：

1. 所需要的宏包：\usepackage{graphicx}

2. [htbp] 为调整图片排版位置选项，说明如下：

   [h]当前位置。将图形放置在正文文本中给出该图形环境的地方。如果本页所剩的页面不够，这一参数将不起作用。 [t]顶部。将图形放置在页面的顶部。 [b]底部。将图形放置在页面的底部。 [p]浮动页。将图形放置在一只允许有浮动对象的页面上。

3. [htbp]选项是\(\LaTeX\)自动排版的，会导致后来写的文本自动紧接着前面的文本。如果需要指定图片在当前位置，就需要

   1. 引入宏包\usepackage{float}
   2. \begin{figure}[H]

排版两张图片在同一行

\begin{figure}[H]
    \centering
    \begin{minipage}[t]{0.48\textwidth}
    \centering
    \includegraphics[width=6cm]{fig/Figure3-Female-Height.png}
    \label{fig_22}
    \caption{Female Height}
    \end{minipage}
    \begin{minipage}[t]{0.48\textwidth}
    \centering
    \includegraphics[width=6cm]{fig/Figure2-Male-Height.png}
    \caption{Male Height}
    \label{fig_23}
    \end{minipage}
\end{figure}

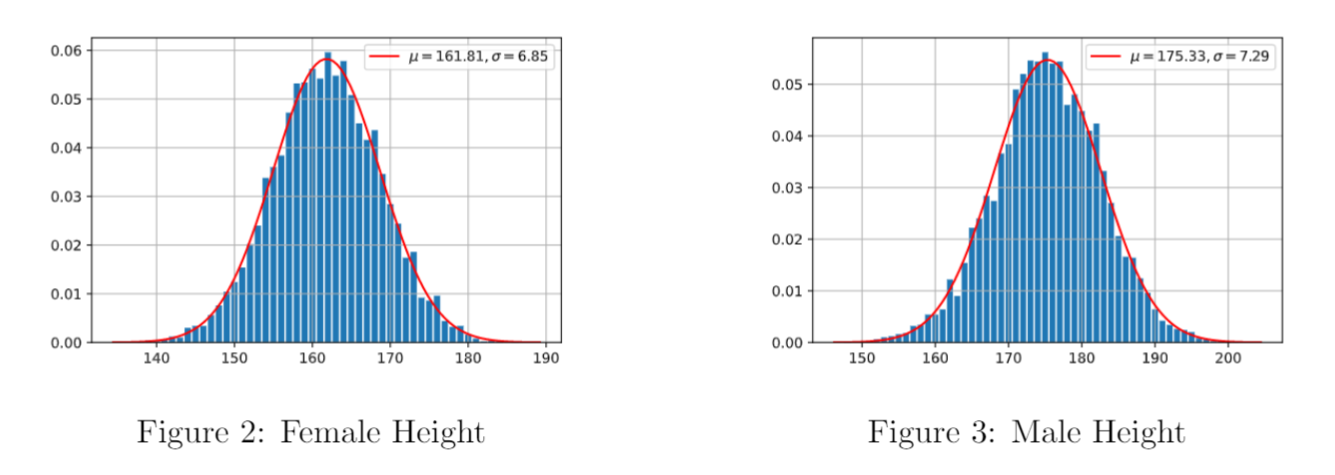
基本用法和插入单张图片非常相似，主要的区别是多了minipage的使用。

参考资料

Latex如何插入图片

Latex 并排插入两张图片

[LaTeX] 用minipage来排版多张图片（子图片）！ （以及用subfigure而不是subfloat来排版代码型图片）

\(\LaTeX\)定理、引理、证明

定理

\newtheorem{thm}{\bf Theorem}[section]
\begin{thm}\label{thm1}
    Let $f_1$ and $f_2$ be normal densities with respective means $\mu_1$ and $\mu_2$ and common variance $\sigma^2$, and let $f$ be the 
    mixture density $0.5 f_1+0.5 f_2$. Then $f$ is unimodal if and only if $|\mu_2-\mu_1 | \leq  2\sigma$. [4]
\end{thm} 

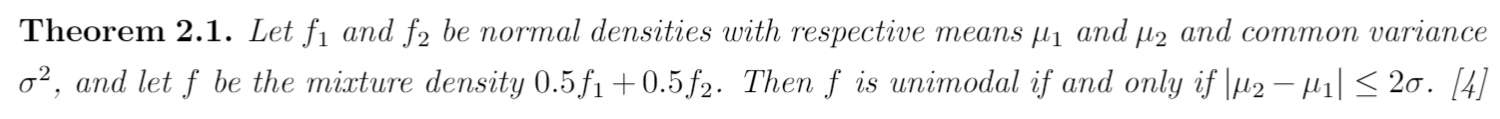
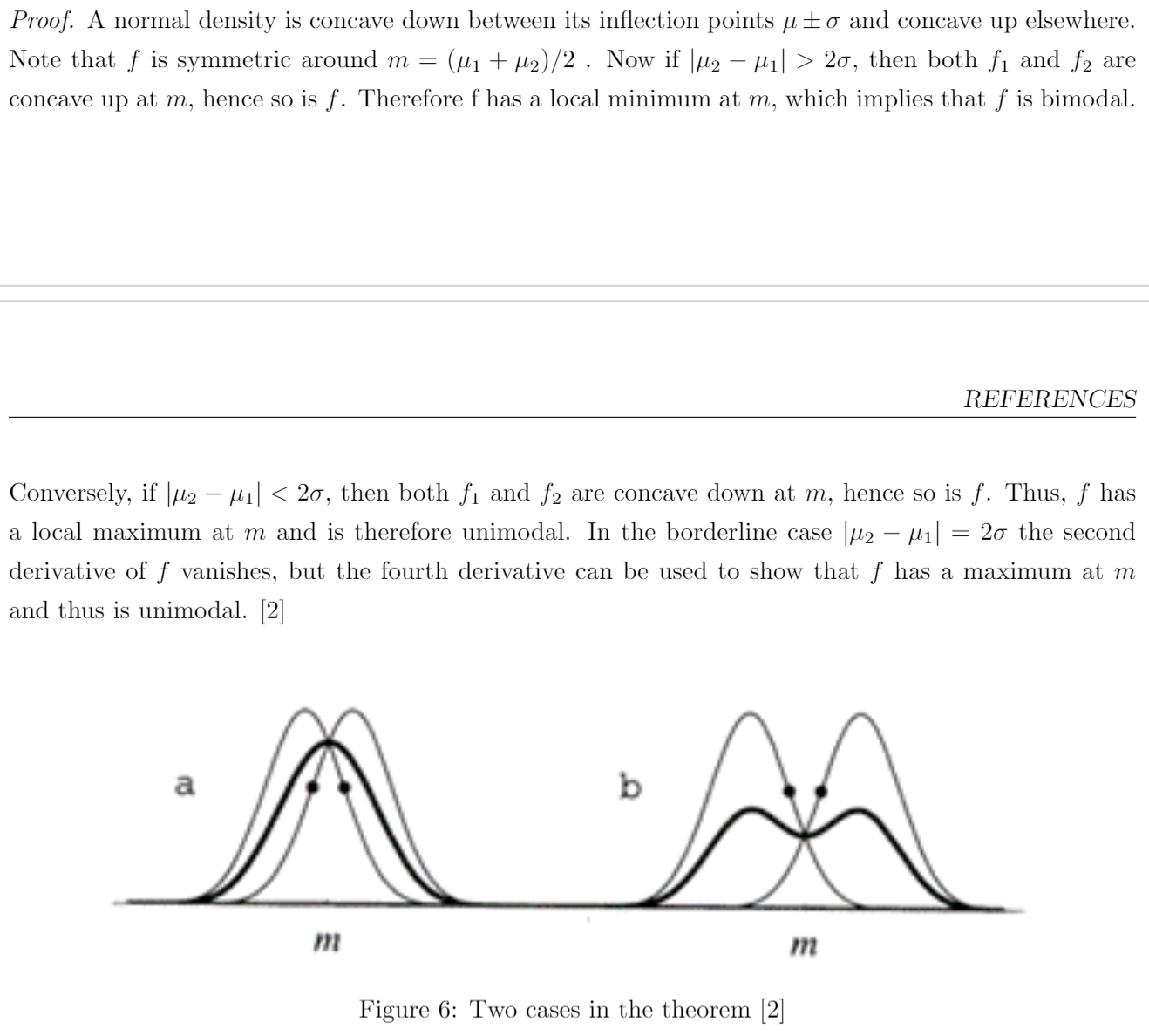
证明

\begin{proof}
    A normal density is concave down between its inflection points $\mu \pm \sigma$ and concave up elsewhere. Note that $f$ is symmetric 
    around $m=(\mu_1+\mu_2)/2$ . Now if $|\mu_2-\mu_1 |>2\sigma$, then both $f_1$ and $f_2$ are concave up at $m$, hence so is $f$. Therefore f has a 
    local minimum at $m$, which implies that $f$ is bimodal. Conversely, if $|\mu_2-\mu_1 |<2\sigma$, then both $f_1$ and $f_2$ are concave down 
    at $m$, hence so is $f$. Thus, $f$ has a local maximum at $m$ and is therefore unimodal. In the borderline case $|\mu_2-\mu_1 |=2\sigma$ the 
    second derivative of $f$ vanishes, but the fourth derivative can be used to show that $f$ has a maximum at $m$ and thus is unimodal. [2]
    \begin{figure}[H]
        \centering
        \includegraphics[width=14cm]{fig/proof.png}
        \caption{Two cases in the theorem {[2]}}
    \end{figure}
\end{proof}

参考资料

Latex中定理、引理、证明、假设