图形学入门笔记4: 实时阴影

发表于 2023-06-04 更新于 2025-01-04 分类于 GameGraphics 阅读次数：本文字数： 5.7k 阅读时长 ≈ 5 分钟

Shadow Map

Shadow Map的思想非常简单，就是通过两个Pass将阴影渲染出来。在第一个Pass中，从光源的视角去渲染场景，记录片元的深度，得到一张深度图。然后进行第二个Pass，从摄像机的视角去渲染场景，对于渲染的每一个片元，将其坐标转化为以光源为参照的坐标，可以得到当前的深度，将这个深度值和存储在深度图中的深度值进行比较，如果说当前深度大于深度图中的深度，说明这个位置的光源被物体遮挡了，是一个阴影。

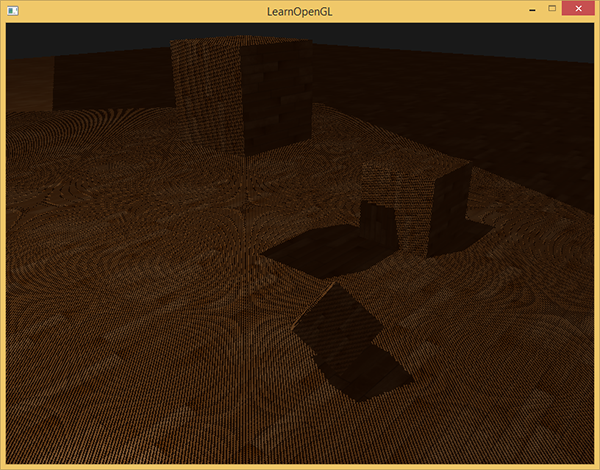
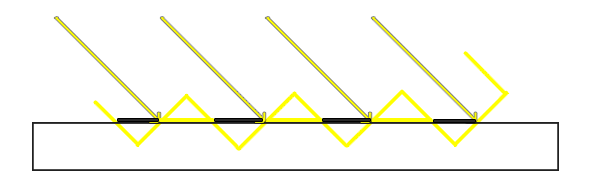
但是，Shadow Map会造成摩尔纹的问题，如下图所示。这是由于采样率不足，多个不同位置但临近的片元有可能映射到同一个ShadowMap的像素上，如第二张图所示，这就会导致有些像素会被误认为是阴影（产生了错误的自遮挡）。为了解决这个问题我们可以增加一个非常小的bias，就好像让地面稍微悬空一点，让那些自遮挡的部分不被误判为阴影，这样子就可以解决摩尔纹的问题了。但同时，这样子做又会引出新的问题，就是物体看起来像是和地面悬空了一样。实际上有很多不同设置bias大小的办法。

比较简单的一种自适应bias方法是通过法线和入射光的夹角来确定。当入射光非常倾斜的时候，我们需要的bias是比较大的，反之会比较小。所以我们可以通过设定一个bias的最大值和最小值，然后通过法线和入射光的夹角使bias取一个合适的值。

更具体的，还可以采用更加细致的数学计算，可以参考自适应Shadow Bias算法 - 知乎中给出的公式。注意以上两种方法中，要考虑法线方向和光线方向在不同侧，会有负值，所以需要加一个abs（比如说小女孩的背面）。

PCF

PCF全称是Percentage Closer Filtering，是为了解决锯齿问题的一种最简单的处理方法。顾名思义，这种方法是采用了filtering的方法，当计算某个像素是否被遮挡时，首先先采样以该像素为中心周围一些点的遮挡情况，最后的Visibility值为被遮挡的采样点的比率。也就是说，对于每一个shading point，我们都要在shadow map上这个点周围一个范围内采样深度，并且判断和渲染视角深度的关系

Note

注意这里的filtering操作是在计算可见度的时候进行的操作，并非是直接在深度图上进行的操作（直接在深度图上进行卷积最终计算的结果还是硬阴影，没有意义）。

float PCF(sampler2D shadowMap, vec4 coords, float biasC, float filterRadiusUV) {
  //uniformDiskSamples(coords.xy);
  poissonDiskSamples(coords.xy); //使用xy坐标作为随机种子生成
  float visibility = 0.0;
  for(int i = 0; i < NUM_SAMPLES; i++){
    vec2 offset = poissonDisk[i] * filterRadiusUV;
    float shadowDepth = useShadowMap(shadowMap, coords + vec4(offset, 0., 0.), biasC, filterRadiusUV);
    if(coords.z > shadowDepth + EPS){
      visibility++;
    }
  }
  return 1.0 - visibility / float(NUM_SAMPLES);
}

PCSS

在PCF中，filtering的范围大小是预先确定的，然而在实际情况中，距离更近的阴影更影，远处则更远，如下图

在PCF的基础上，PCSS会根据阴影距离物体的远近调整filtering的大小。PCSS分为三个步骤：

Blocker Search，在某个特定范围内得出平均遮挡物的深度；
估计半影 (Penumbra)区域的大小，根据相似三角形得出；
使用计算得到的半影大小作为FilterRadius进行PCF

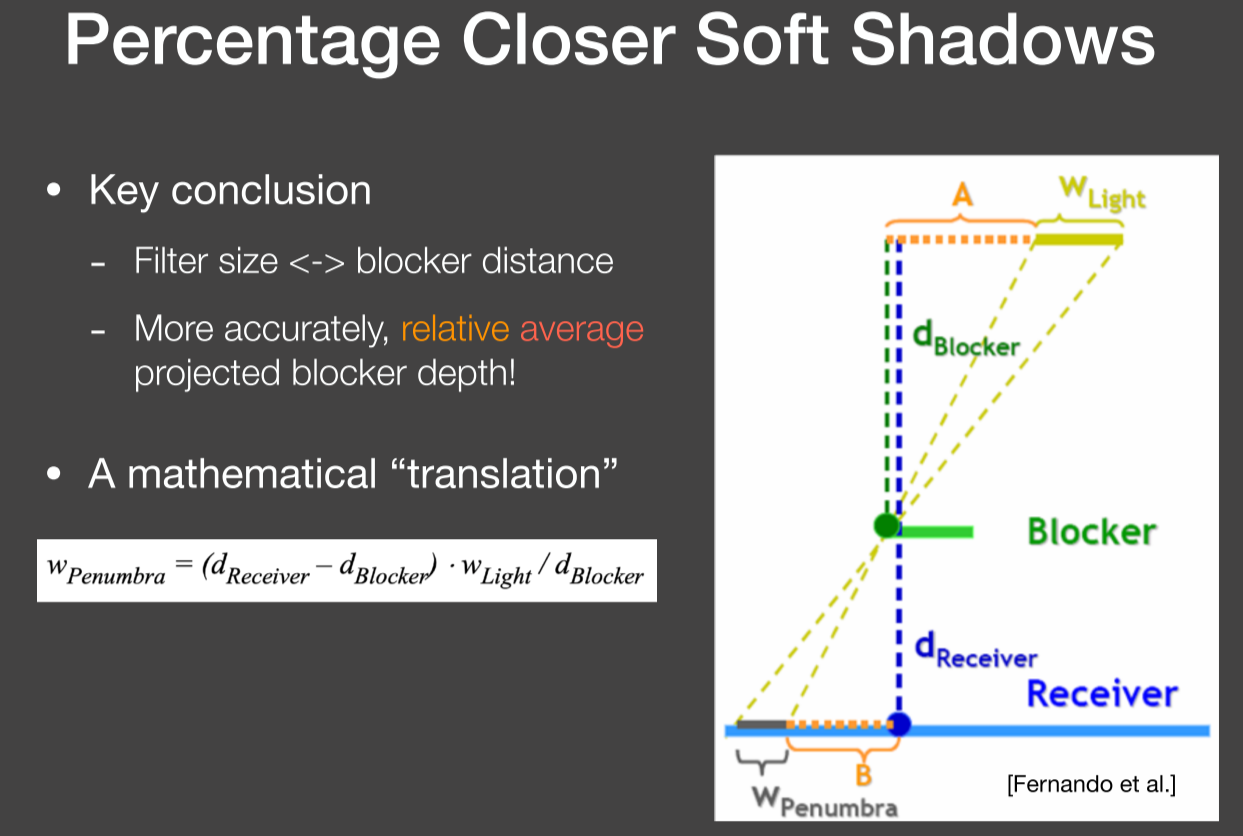
那么在第一步中，在哪一块区域中计算那遮挡物的平均深度呢？这块区域取决于光源的大小和阴影接收平面距离光源的距离。同样类似的，根据相似三角形，在shadow map上可以得到对应的区域，如下图所示

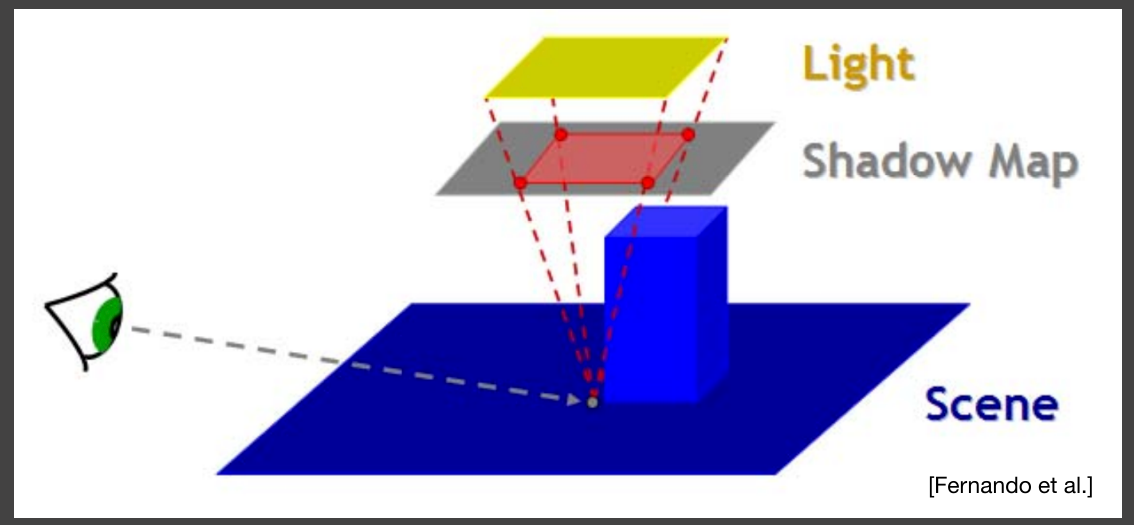
对应的代码实现

float findBlocker(sampler2D shadowMap, vec2 uv, float zReceiver) {

  int blockerNum = 0;
  float blockDepth = 0.;
  float posZFromLight = vPositionFromLight.z;
  // blocker search的大小
  // NEAR_PLANE是近平面，即shadow map所在的平面
  float searchRadius = LIGHT_SIZE_UV * (posZFromLight - NEAR_PLANE) / posZFromLight;

  poissonDiskSamples(uv);
  for(int i = 0; i < NUM_SAMPLES; i++){
    float shadowDepth = unpack(texture2D(shadowMap, uv + poissonDisk[i] * searchRadius));
    if(zReceiver > shadowDepth){
      blockerNum++;
      blockDepth += shadowDepth;
    }
  }
  if(blockerNum == 0)
    return -1.;
  else
    return blockDepth / float(blockerNum);
}

float PCSS(sampler2D shadowMap, vec4 coords, float biasC){
  float zReceiver = coords.z;

  // STEP 1: avgblocker depth
  float avgBlockerDepth = findBlocker(shadowMap, coords.xy, zReceiver);
  if(avgBlockerDepth < -EPS)
    return 1.0;

  // STEP 2: penumbra size
  float penumbra = (zReceiver - avgBlockerDepth) * LIGHT_SIZE_UV / avgBlockerDepth;
  float filterRadiusUV = penumbra;

  // STEP 3: filtering
  return PCF(shadowMap, coords, biasC, filterRadiusUV);
}

Variance Soft Shadow Mapping (VSSM)

VSSM在PCF和PCSS的基础上通过统计学方法进行了改进。

Step 3

在PCSS中第三步即PCF中，我们需要对任意一个shading point通过卷积计算其visibility。这一步通常比较耗时。我们可以将其转化为一个概率，其中可以代表shadowmap的采样值，可以表示shading point的深度。我们可以将深度的概率分布粗略的估计为一个Gaussian distribution，更进一步的，我们甚至可以直接采用Chebyshev不等式进行估计

接下来的问题就是如何计算均值和方差，对于方差我们可以利用公式，这样就只需要知道均值以及平方的均值就可以计算方差

Step 1

在PCSS第一步Blocker search中，我们也需要对shadow map进行采样来计算遮挡物的平均深度，同样也是非常耗时的步骤。这里同样可以用概率进行估计以提高效率。首先定义以下相关变量

遮挡物 ()的平均深度
非遮挡物 ()的平均深度
总样本数量
遮挡物的样本数量
非遮挡物的样本数量
区域平均深度

因此我们有以下公式

使用概率作以下估计和假设
然后就可以用Chebyshev不等式解决。另外这里使用的假设直接假定非遮挡物都和shading point在同一平面上，可以理解为因为绝大部分阴影接收者都是一个平面，所以这样的假设也具有一定的合理性。

到此为止，用统计学方法，我们可以解决PCSS中两步采样较为耗时的问题。

MIPMAP and Summed-Area Variance Shadow Maps

在具体实现算法的时候，我们需要计算shadow map中一块区域的方差和均值，可以通过Mipmap或者SAT(Summed Area Table)实现。

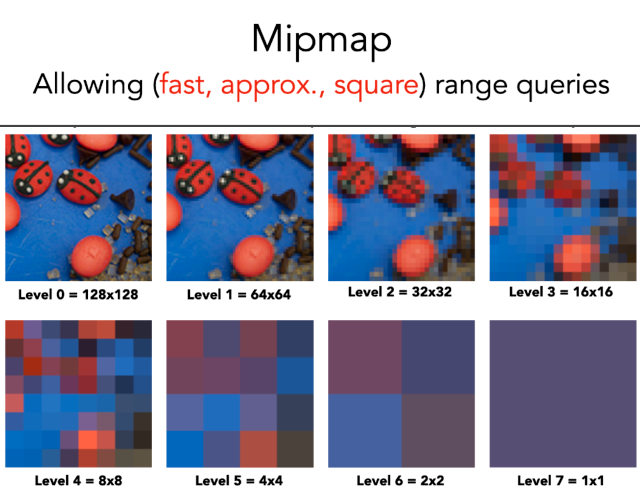
Mipmap可以快速的对Texture进行范围查询，在查询某块方形范围时，需要根据方形大小选择对应的Level，根据方形中心位置选择周围四个像素进行插值，以及上下Level之间作三线性插值(Trillinear interpolation)。由于多次插值，所以得到的结果是不准确的。另外，Mipmap不适合做非方形区域的范围查询。

SAT使用了类似前缀和的思想，维护一个table，每个位置上存储从原点到当前位置的矩形区域的和，如下图所示，可以很方便的得到某一块区域的范围之和。预计算和存储所需要的额外复杂度都是(逐行逐列累加)，可以采用并行计算进行加速。SAT得到的结果对比Mipmap是准确的，但缺点就是预处理比较耗时。

问题

由于VSSM中使用了大量的假设，在这些估计不准确的时候，会造成渲染的结果存在明显的artifact。比如由于我们假设了在filtering的范围内的深度是一个正态分布，但如果在并不是的情况下，就会造成估计的结果不准确。通常有两种情况，过大或者过小。过小会导致画面偏黑，而过大会导致漏光的现象，比如下面一个例子

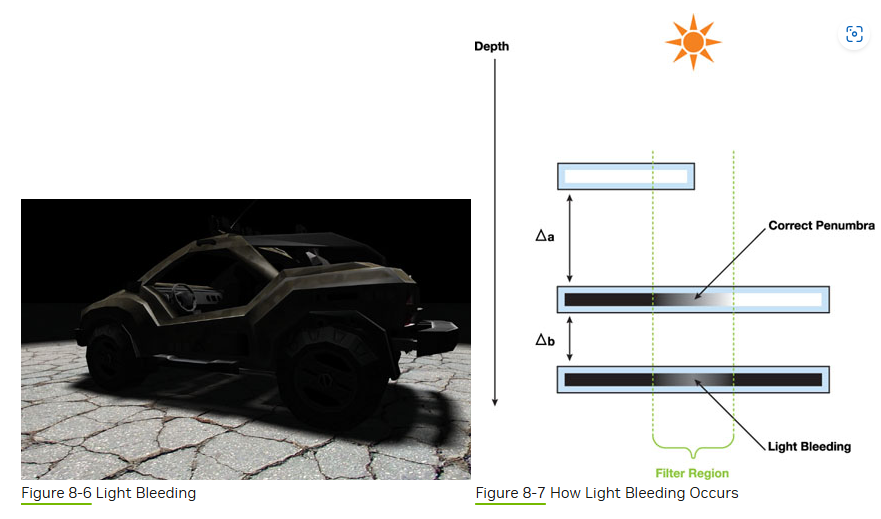
假设右图中三块板从上到下A、B、C的深度分别为a、b、c，那么在Filter region中我们计算得到深度的均值和方差

因此，根据Chebyshev不等式，B板的Visibility就是

C板的Visibility是

可以看出当很小时，也就是多个遮挡物体之间的深度变化很大的时候，本来应该很小的Visibility在上面的例子中会接近0.5，就会造成漏光问题。

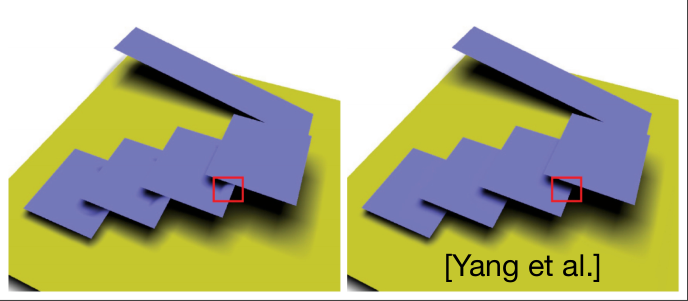
除了这个问题以外，另一个假设，也就是假设未造成遮挡的物体和阴影接收平面处于同一个平面上，在一些并不符合的情况下就会造成漏光的问题，如下图。

Moment Shadow Map

为了解决VSSM中存在的问题，Moment Shadow map使用了更高阶的矩(Moment)去拟合一个分布的CDF。Moment shadow mapping使用矩的最简单的形式 VSSM在本质上就是使用了两阶的Moment,

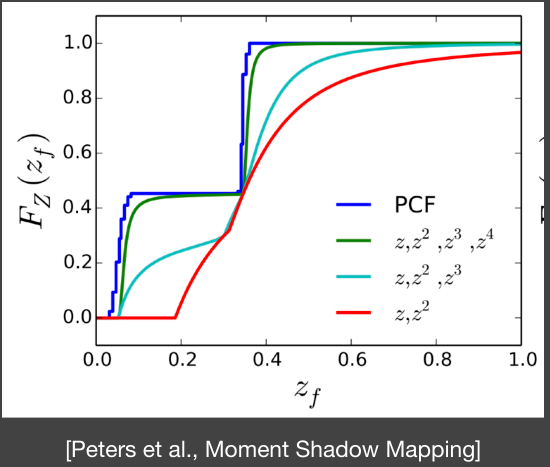
从图中可以看到，通常情况下四阶moment已经可以很好的拟合一个CDF了。但是虽然 Moment Shadow Mapping 效果相当不错，很好的解决了 VSSM 绝大部分缺陷，但是它仍需要相当的额外空间开销和重建矩的额外性能开销。

Distance Field Soft Shadow

Distance Field Shadow Map采用了Signed Distance Function (SDF)进行阴影的计算。使用SDF可以有效解决Shadow map存在的诸多问题，比如摩尔纹，peter panning，锯齿等等问题。

SDF用一个Volume Texture存储每个点到最近的mesh表面的距离，如果在mesh外则为正，在mesh内部则为负。

SDF的性质可以用于进行ray tracing。从起点出发，每一次trace步进当前点查询到的最近距离，这样子可以确保每一次步进都不会穿过物体。下图展示了从起点不断trace光线直到找到了光线和树的交点的过程。

使用这个性质，可以通过ray marching的方式可以大致估算出visibility。如下图所示，假设有一个面光源，从shading point出发，trace一根光线，使用SDF可以计算出这根光线在多大角度的范围内没有被遮挡，越小的角度代表越小的visibility。具体做法是，从起点出发，按照上面的办法不断的trace光线，在这个过程中计算角度，也就是

但在实际情况下，由于计算比较耗时，可以粗略的通过简单的线性关系表示遮挡程度，而并非严格的计算未遮挡角度和光源最大角度的比值

其中用来控制阴影的软硬程度，如下图所示

shader代码实现如下，来源Inigo Quilez :: computer graphics, mathematics, shaders, fractals, demoscene and more

float softshadow( in vec3 ro, in vec3 rd, float mint, float maxt, float k )
{
    float res = 1.0;
    float t = mint;
    for( int i=0; i<256 && t<maxt; i++ )
    {
        float h = map(ro + rd*t);
        if( h<0.001 )
            return 0.0;
        res = min( res, k*h/t );
        t += h;
    }
    return res;
}