Postion Based Dynamics软体模拟
在position based dynamics中,物体由许多的粒子组成,这些粒子之间有许多约束,比如说距离约束、体积约束等等。在物体运动的过程中,通过解这些约束来更新粒子的位置。大致的伪代码如下(这是XPBD的伪代码,XPBD的区别在于XPBD使用了substep加速收敛)

Solve Constraint
对于每个Constraint,计算其位置的便宜量\(\Delta\mathbf{x}_{i}=\lambda w_{i} \nabla C_{i}\) \[ \lambda=\frac{-C}{w_{1}\vert\nabla C_{1}\vert^{2}+w_{1}\vert\nabla C_{1}\vert^{2}+\cdots+w_{n}\vert\nabla C_{n}\vert^{2}+ \frac{\alpha}{\Delta t^{2}}} \]
- \(C\) 是约束函数
- \(\nabla C_{i}\) 是约束函数关于\(x_{i}\) 的gradient
- \(w_{i}\)是粒子的质量的倒数
- \(\alpha\) 是stiffness参数
| Distance | Volume |
|---|---|
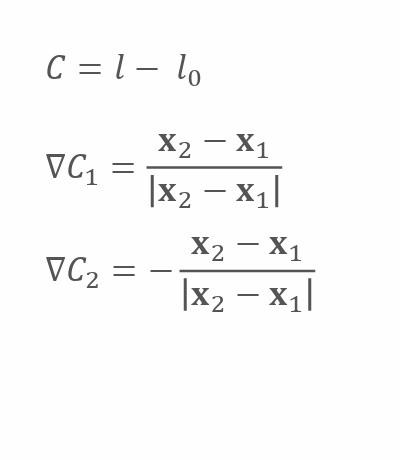 |
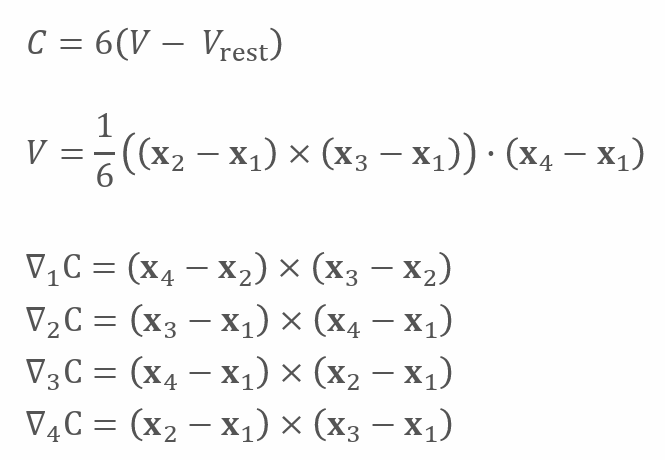 |
碰撞检测
碰撞检测分为broad phase和narrow phase,在broad phase使用BVH和Spatial Hash等空间加速算法排除掉大部分不需要进行检测的三角形(由于时间限制,我们并没有完成这一部分,这也就导致最后的simulator无法实时运行)。对于有可能相交的三角形进行两两检测,然后通过Collision Constraint修正顶点的位置。
根据Paper中的描述,Collision Constraint定义为 \[ C(\mathbf{p})=(\mathbf{p}-\mathbf{q}_{c}) \cdot \mathbf{n}_{c} \] \(\mathbf{q}_{c}\)是从\(p_{t-1}\rightarrow p_{t}\) 的线段和triangle的相交点(entry point),\(\mathbf{n}_{c}\)是相交点处的法线。Collision Constraint通求解显然就是\(p_{t}\)在相交平面上的投影(沿着gradient方向进行移动)。
当然还有特殊情况比如说,我们在某一时刻碰撞检测失效了,那么这个时候\(p_{t-1}\)和 \(p_{t}\)就都在另一个mesh内部了。对于这种情况,Paper中说这个时候的Constaint就变成了 \[ C(\mathbf{p})=(\mathbf{p}-\mathbf{q}_{s}) \cdot \mathbf{n}_{s} \] \(\mathbf{q}_{s}\)是\(p_{t}\)最近平面的投影点,\(\mathbf{n}_{s}\)是法线,类似的,也就是说我们需要找到当前顶点位置的最近平面然后投影过去。
对于判断点是否在mesh内部,可以采用射线法,计算出相交点的个数进行判断。这里就产生了一个问题,我们的Tetrahedron的生成貌似有点点问题,所以导致我们无法获得表面的三角形(在Tetrahedron内部有一些三角形的残余不知道为什么)。
Tetrahedron的生成
Tetrahedron的生成可以使用Incremental Delaunay Method生成。四面体可以近似的使用平面的三角形进行类比,只需要将四面体的四个顶点换成三个顶点。一个Delaunay网格中的任意一个点都不在除了他坐在的三角形其他的三角形的外接圆中。
Wiki In mathematics and computational geometry, a Delaunay triangulation (DT), also known as a Delone triangulation, for a given set {p_i} of discrete points p_i in general position is a triangulation such that no point p_i is inside the circumcircle of any triangle in the DT. Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles.
Delaunay算法流程如下
- 输入:mesh的顶点坐标
- 首先用四个临时坐标生成一个大的四面体将所有的点围起来
- 然后重复以下流程
- 将一个新的vertex添加进去
- 移除所有的外接圆包含这个vertex的四面体
- 以这个vertex为中心,生成环在其周围的四面体,填补将上一步移除造成的空缺
- 最后将临时点移除即可
移除四面体时,需要先找到这个点在哪个tetrahedron内部。这可以通过该点发出一条到上一个添加的点的射线,找到第一个相交的surface。然后通过flood-fill去找到附近的不符合条件的四面体。 # 并行化 由于Position Based Dynamics采用的是Gauss-Siedel Iteration,这导致了很难将其并行化,所以无法在taichi的gpu mode下运行。如果想要并行化的话,需要使用Jacobi Iteration。然而从效率上来说,Jacobi Iteration的收敛速度是远远不如Gauss-Sidel的。还有一种方式是Graph-Coloring Methods。
Graph Coloring的思想是,将所有的constaint分成多个phase进行求解。在每一个phase,我们需要确保没有任何一个costraint共享一个顶点。这就对应着graph coloring问题。
最终效果
由于Blender的Tetrahedralize算法生成的四面体似乎有点问题,导致碰撞检测并不robust。最后时间问题,并行化只实现了Jacobi,但是效果还是没有Gauss-Siedel好。Broad Phase的碰撞检测也有待完成。参数也调整的比较stiff,效果如下
