Quaternion四元数详解

发表于 更新于 分类于 阅读次数： 本文字数： 2.8k 阅读时长 ≈ 3 分钟

四元数(Quaternion)是用于表示旋转的一种方式，其相比于Rotation Matrix的好处在于能够更轻松的插值、不存在万向节(gimbal lock)的问题。其定义如下： \[ q=a+bi+cj+dk \] 其中\(i^{2}=j^{2}=k^{2}=ijk=-1\)。同时也可以用以下方式表示： \[ q=\left(a, \mathbf{v}\right), \text{where }\mathbf{v}=\begin{bmatrix}b\\c\\d\end{bmatrix} \] \(a\)是实部，\(\mathbf{v}\)是向量。四元数的旋转可以理解为四维坐标在三维空间中的投影，具体可以参考3b1b的视频

四元数的基本运算

  • 共轭 (Conjugate) \[ q^{*}=a-bi-ci-dk \]

  • 逆 (Inverse) \[ \begin{align*} q^{-1}=\frac{q^{*}}{\Vert q \Vert}\\ q^{-1}q=qq^{-1}=1 \end{align*} \]

  • 模 (Norm) \[ \Vert q \Vert=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}} \]

  • 乘法 \[ pq=\begin{bmatrix}(p_{a}\mathbf{q}_{V}+q_{a}\mathbf{p}_{V}+\mathbf{p}_{V}\times \mathbf{q}_{V})&(p_{a}q_{a}-\mathbf{p}_{V}\cdot \mathbf{q}_{V})\end{bmatrix} \]

  • 当\(\Vert q \Vert=1\)时，\(q^{-1}=q^{*}\)

  • \((pq)^{*}=q^{*}p^{*}\)

  • \((pq)^{-1}=q^{-1}p^{-1}\)

如何使用四元数表示旋转

四元数表示旋转时必须时unit quaternion，表示如下 \[ \begin{align*} q&=\begin{bmatrix}q_{a}&\mathbf{q}_{V}\end{bmatrix}\\ &=\begin{bmatrix}\cos{\frac{\theta}{2}} & \mathbf{v} \sin{\frac{\theta}{2}}\end{bmatrix} \end{align*} \] 其中\(a^{2}+b^{2}+c^{2}+d^{2}=1\)

如果想要对空间中的点进行旋转，需要先将点(或向量)的三维坐标形式转化为quaternion的形式： \[ v=\begin{bmatrix}0&\mathbf{v}\end{bmatrix}=\begin{bmatrix}0&v_{x}&v_{y}&v_{z}\end{bmatrix}=bi+cj+dk \] 对该点的四元数旋转表示如下： \[ v'=qvq^{-1}=qvq^{*} \]

四元数和旋转矩阵的相互转化

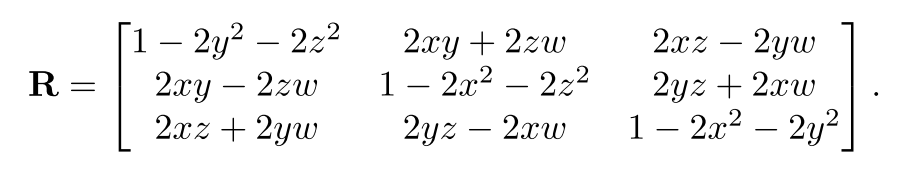
  • Quaternion to Matrix image.png
  • Rotation Matrix to Quaternion 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    // From Game Engine Architecture
    void matrixToQuaternion(
    		const float R[3][3],
    		float       q[/*4*/])
    {
    	float trace = R[0][0]+R[1][1]+R[2][2];

    	// check the diagonal
    	if (trace > 0.0f)
    	{
    		flaot s = sqrt(trace + 1.0f);
    		q[3] = s * 0.5f;
    		float t = 0.5f / s;
    		q[0] = (R[2][1] - R[1][2]) * t;
    		q[1] = (R[0][2] - R[2][0]) * t;
    		q[2] = (R[1][0] - R[0][1]) * t;
    	}
    	else
    	{
    		// diagonal is negative
    		int i = 0;
    		if (R[1][1] > R[0][0]) i = 1;
    		if (R[2][2] > R[i][i]) i = 2;
    		static const int NEXT[3] = {1, 2, 0};
    		int j = NEXT[i];
    		int k = NEXT[j];
    		float s = sqrt((R[i][j] - (R[j][j]+R[k][k])) + 1.0f);
    		q[i] = s * 0.5f;
    		float t;
    		if (s != 0.0f) t = 0.5f / s;
    		else           t = s;
    		q[3] = (R[k][j] - R[j][k]) * t;
    		q[j] = (R[j][i] - R[i][j]) * t;
    		q[k] = (R[k][i] - R[i][k]) * t;
    	}
    }

四元数的插值

  • Linear Interpolation (Lerp) \[ q_{\text{LERP}}=\text{LERP}(\mathbf{q}_{A},\mathbf{q}_{b},\beta)=\frac{(1-\beta)\mathbf{q}_{A}+\beta \mathbf{q}_{B}}{\vert(1-\beta)\mathbf{q}_{A}+\beta \mathbf{q}_{B}\vert} \]
  • Spherical Linear Interpolation (Slerp) \[ \text{SLERP}(\mathbf{p},\mathbf{q},\beta)=w_{p}\mathbf{p}+w_{q}\mathbf{q} \] 其中 \[ \begin{align*} w_{p}&=\frac{\sin(1-\beta)\theta}{\sin \theta} \\ w_{q}&=\frac{\sin\beta\theta}{\sin \theta} \end{align*} \] \(\mathbf{p}\)和\(\mathbf{q}\)的夹角可以通过四元数的点乘来计算 \[ \begin{align*} \cos \theta&=\mathbf{p} \cdot \mathbf{q}=p_{x}q_{x}+p_{y}q_{y}+p_{z}q_{z}+p_{w}q_{w}\\ \theta&=\cos^{-1}(\mathbf{p} \cdot \mathbf{q}) \end{align*} \]

参考资料

  1. Visualizing quaternions, an explorable video series
  2. Quaternions and 3d rotation, explained interactively - YouTube
  3. Game Engine Architecture 4.4 Quaternions
  4. Games104 Lecture 08