实时渲染笔记-Importance Resampling and ReSTIR

发表于 2025-01-04 分类于 GameGraphics 阅读次数：本文字数： 6.2k 阅读时长 ≈ 6 分钟

Resampled importance sampling (RIS)

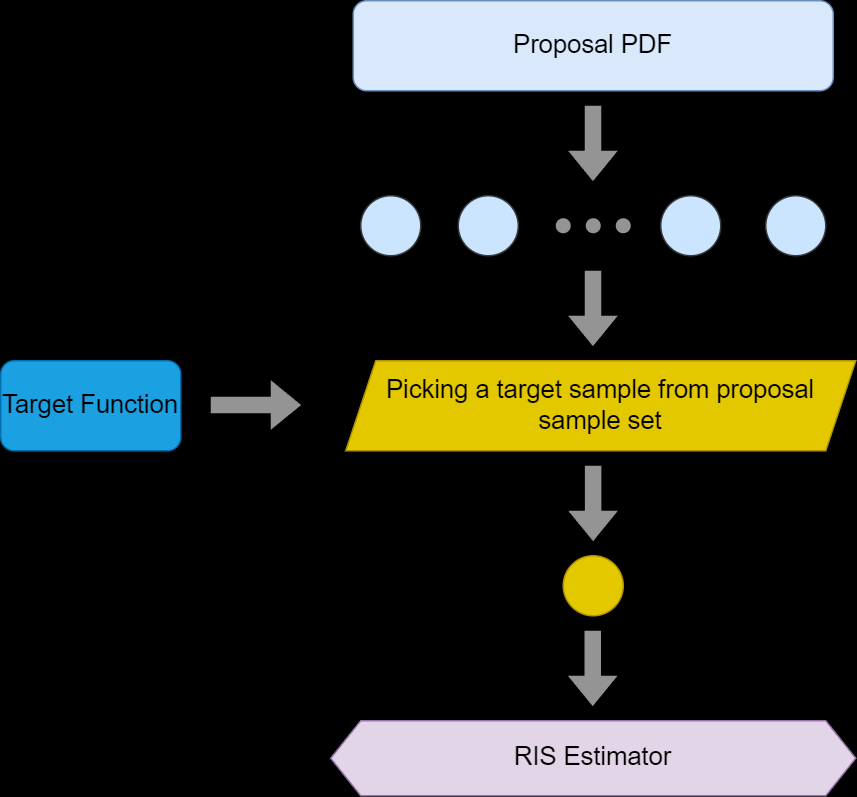
RIS算法流程

RIS流程:

从一个易于采样的分布(proposal PDF) \(p(x)\)上，进行采样，抽取\(M\)个样本
得到一个期望进行拟合的真实目标概率分布(target PDF) \(\hat p(x)\)
对于每一个抽取的样本，分配权重\(w(x)={\hat p(x)}/{p(x)}\)，进而得到每个样本的条件概率，通过这种方式进行采样的方法叫做重要性重采样Sampling importance resampling (SIR)
采样出来的结果可以用于1-sample RIS estimator

\[ \langle L \rangle = \frac{f(y)}{\hat p(y)} \cdot \left( \frac{1}{M}\sum\limits_{j=1}^{M}w(x_{j}) \right) \]

多次进行RIS采样，从样本池中的\(M\)个样本（可以重新生成样本池，也可以直接在同一个样本池中进行采样进行简化）中有放回的采样\(N\)个样本，得到最终的结果

\[ \langle L \rangle = \frac{1}{N} \sum\limits_{i=1}^{N}\left(\frac{f(y_{i})}{\hat p(y_{i})} \cdot \left( \frac{1}{M}\sum\limits_{j=1}^{M}w_{i}(x_{ij}) \right) \right) \]

其中\(\hat{p}(y)/\frac{1}{M}\sum\limits_{j=1}^{M}w(x_{j})\) 是SIR PDF，也就是修正过后的真实的采样的PDF

通过RIS方法进行采样好处是可以近似的采样任意的概率分布，比如我们在ReSTIR算法中可以将\(L(\omega)f_{r}(\omega_{o}, \omega_{i})\cos{\theta_{i}}\)，也就是rendering equation中除去visibility的光照贡献，论文中称之为unshadowed illumination作为目标函数（对这个概率分布采用传统采样方法是无法实现的，因为无法进行归一化，PDF是无法计算出来的）

下面两张图展示了RIS的伪代码和流程

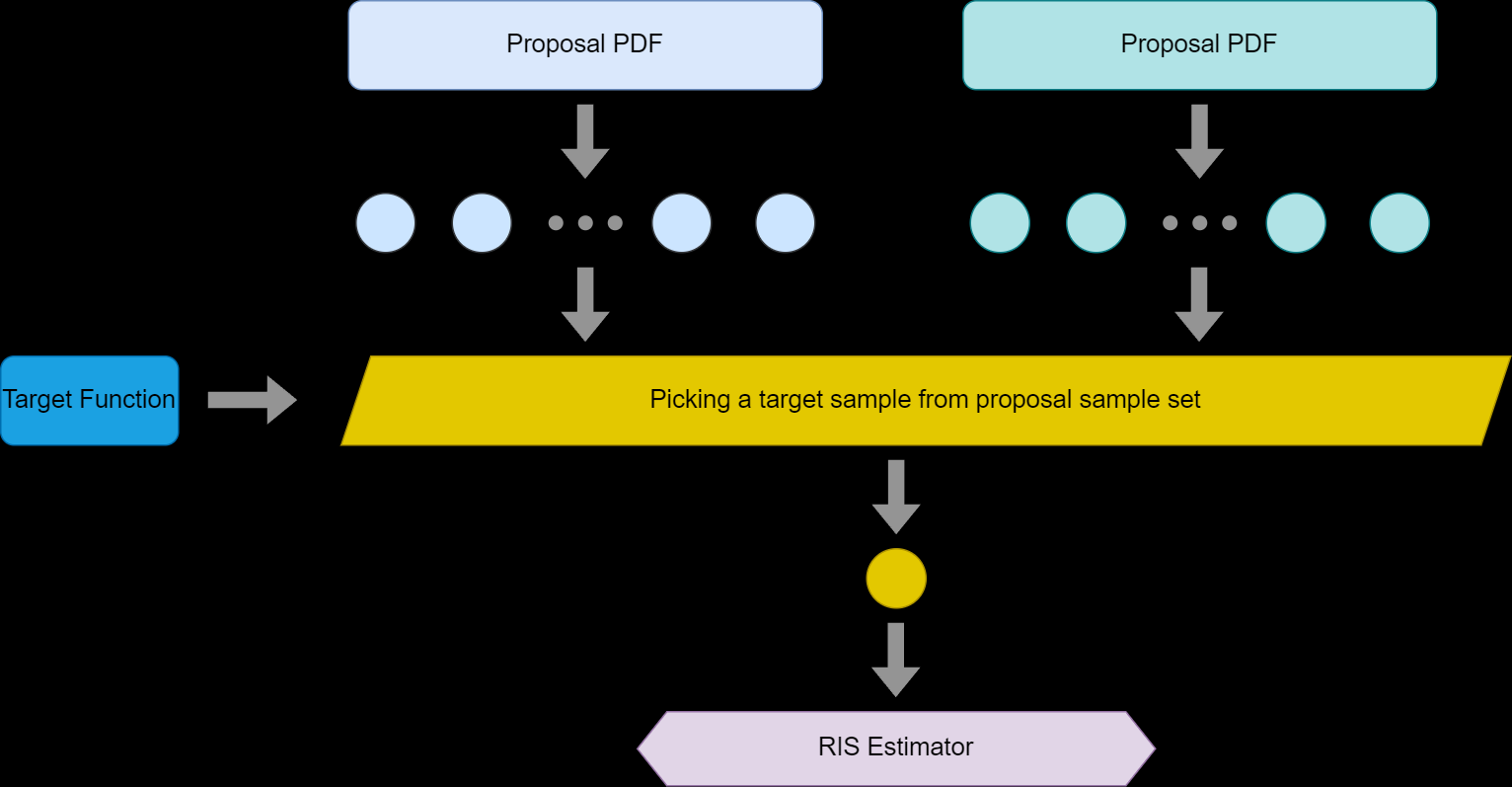
RIS和MIS相结合

在使用RIS的同时，也可以采用MIS，进一步降低方差，达到更好的效果。这里通常有两种结合的方式。

第一种方法 第一步的时候，可以直接采用MIS的方式在两个概率分布上进行采样，得到两组采样后的结果。在这种情况下，分配权重的时候就需要考虑使用MIS的结果。正如 GRIS 论文中指出的，每个proposal PDF 的权重可以推广到这种形式 \[ w_{i}(x)=m_{i}(x)\frac{\hat p(x)}{p_{i}(x)} \] 其中\(m_{i}(x)\)代表的是MIS中采用的权重，一般常用的是balanced heuristic [[Computer Graphics Review#Multiple Importance sampling]]，形式如下： \[ w_{s}(x)=\frac{N_{s}p_{s}(x)}{\sum\nolimits_{j}N_{j}p_{j}(x)} \]

Luckily, Talbot [2005] showed how to leverage multiple competing techniques using MIS within RIS to reduce variance: generate the pool of proposals using MIS and use the effective MIS (mixture) PDF as the source PDF in the rest of the RIS procedure.

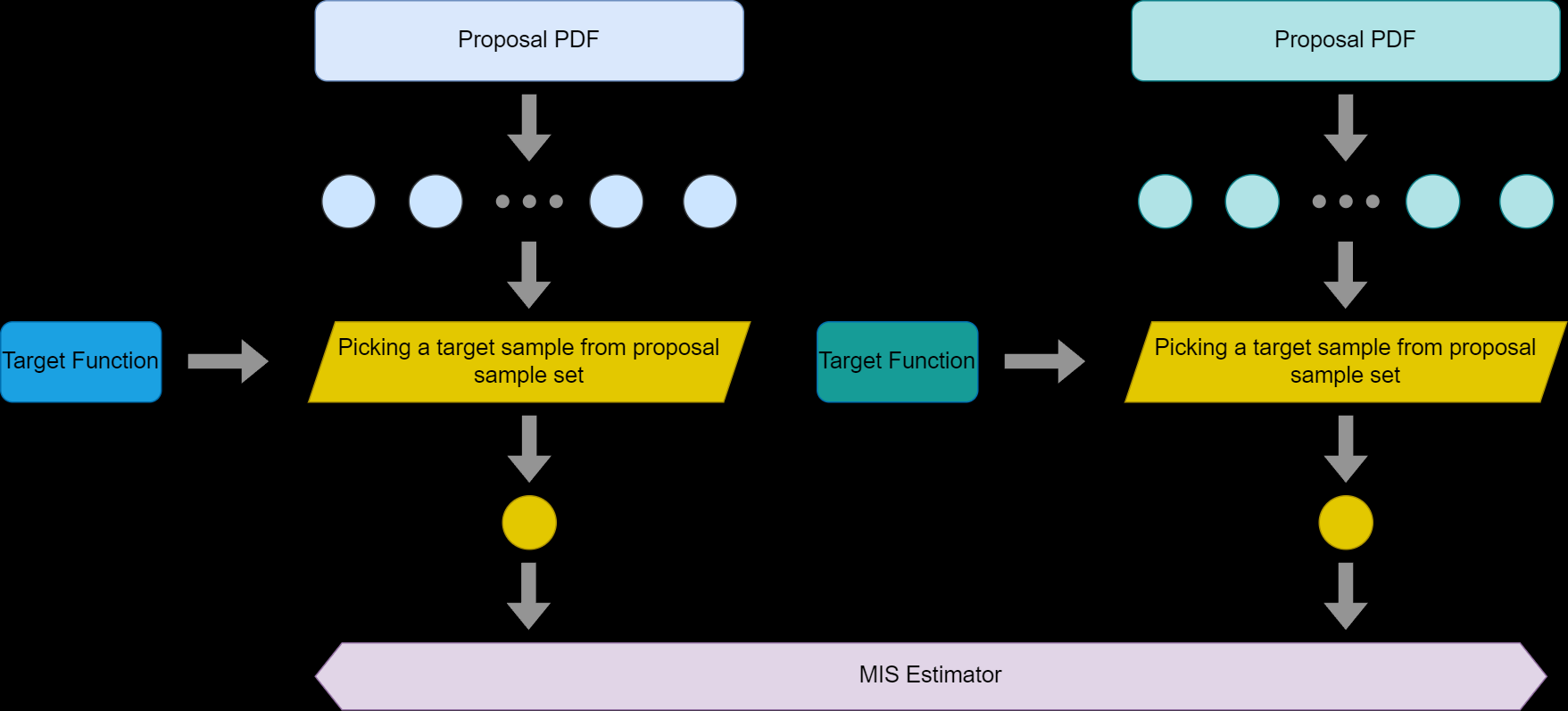
第二种方法

另外我们还可以把SIR视作一种单独的采样方法，然后对于SIR得到的结果之后再进行MIS

RIS的无偏性推导

首先需要证明RIS是无偏的，我们只需要证明一下结论成立 \[ \mathbb{E}\left( \frac{1}{N}\sum\nolimits_{i=1}^{N} \frac{f(y_{i})}{\hat{p}(y_{i})} \left( \frac{1}{M}\sum\limits_{j=1}^{M}w(x_{ij}) \right) \right) = \int{f(x)} {\mathrm{d}{x}} \] 为了推导方便，这里定义一些简化的表示以及回顾之前的一些公式以及一些需要用到的结论 \[ \begin{align*} W&= \sum\limits_{i=1}^{M}w_{i}(x_{i})\\ w_{i}(x)&= m_{i}(x)\frac{\hat p(x)}{p_{i}(x)}\\ \mathbb{E}\left( X \right) &= \mathbb{E}\left( \mathbb{E}(X|Y) \right) \end{align*} \] 并且由于引入了GRIS，这里新引入的权重\(m(x)\)中包含了归一化的\(1/M\)，因此这里需要忽略 \[ \mathbb{E}\left( \frac{1}{N}\sum\nolimits_{i=1}^{N} \frac{f(y_{i})}{\hat{p}(y_{i})} \left( \sum\limits_{j=1}^{M}w(x_{ij}) \right) \right) = \int{f(x)} {\mathrm{d}{x}} \] 详细推导过程，在Understanding The Math Behind ReStir DI · A Graphics Guy's Note推导的基础上添加了一些中间步骤，不知道理解是否正确。 \[ \begin{align*} &\mathbb{E}\left( \frac{1}{N}\sum\nolimits_{i=1}^{N} \frac{f(y_{i})}{\hat{p}(y_{i})} \left( \sum\limits_{j=1}^{M}w(x_{ij}) \right) \right) \\ =& \frac{1}{N}\sum\limits_{i=1}^{N}\mathbb{E}\left( \frac{f(y_{i})}{\hat{p}(y_{i})} \left(\sum\limits_{j=1}^{M}w(x_{ij}) \right) \right)\\ =& \mathbb{E}\left( \frac{f(y)}{\hat p(y)} \left(\sum\limits_{j=1}^{M}w(x_{j}) \right) \right) = \mathbb{E}\left( \frac{f(y)}{\hat p(y)} W\right)\\ =& \mathbb{E}\left( \mathbb{E}\left( \frac{f(y)}{\hat p(y)}W\middle |x_{1},\cdots x_{k} \right) \right)\\ =& \underbrace{\int \cdots\int}_{M}\mathbb{E}\left( \frac{f(x_{k})}{\hat p(x_{k})}W \right) \prod_{i=1}^{M}p(x_{i}) \mathrm{d}{x_{1}}\cdots \mathrm{d}{x_{M}}\\ =& \underbrace{\int \cdots\int}_{M} \left( \sum\limits_{k=1}^{M}\frac{f(x_{k})}{\hat p(x_{k})}W \cdot p(y=x_{k}\vert x_{1},\cdots, x_{k})\right)\prod_{i=1}^{M}p(x_{i}) \mathrm{d}{x_{1}}\cdots \mathrm{d}{x_{M}} \\ =& \underbrace{\int \cdots\int}_{M} \left( \sum\limits_{k=1}^{M}\frac{f(x_{k})}{\hat p(x_{k})}W \frac{w(x_{k})}{W}\right)\prod_{i=1}^{M}p(x_{i}) \mathrm{d}{x_{1}}\cdots \mathrm{d}{x_{M}} \\ =& \sum\limits_{k=1}^{M}\underbrace{\int \cdots\int}_{M} \left( m_{k}(x_{k}) f(x_{k}) \right)\prod_{i=1\&i \ne k}^{M}p(x_{i}) \mathrm{d}{x_{1}}\cdots \mathrm{d}{x_{M}} \\ =& \sum\limits_{k=1}^{M}\int m_{k}(x_{k})f(x_{k})\mathrm{d}x_{k}\prod_{i=1\&i \ne k}^{M}\int p(x_{i})\mathrm{d}x_{i} \\ =& \int \sum\limits_{k=1}^{M}m_{k}(x)f(x) \mathrm{d}x_{k}=\int f(x) \mathrm{d}x_{k} \end{align*} \]

Weighted Reservoir Sampling (WRS)

WRS算法流程

WRS是一种从一个流(stream)\(\{x_{1}, x_{2}, \cdots, x_{M}\}\)进行流式采样的算法，每个元素有一个对应的权重\(w(x_{i})\)，所以\(x_{i}\)被选中的概率是 \[ P_{i}=\frac{w(x_{i})}{\sum\limits_{j=1}^{M}w(x_{j})} \]

数据结构

最终输出的采样的样本
当前权重之和
当前处理过的样本数量\(M\)

输入：加权样本集合(\(\mathbb{S}\))以及对应权重

流程: 依次遍历集合中所有样本，每次update时更新权重之和，并对当前样本以\(w_{i}/w_{\text{sum}}\)的概率进行样本的替换或保留。

WRS算法可以保证在每一次处理一个新的样本时，选择每一个样本的概率都是满足加权概率的。在处理完第\(m+1\)个样本的时候，前\(m\)个样本中\(x_{i}\)被保留的概率是 \[ \frac{w(x_{i})}{\sum\nolimits_{j=1}^{m}w({x_{j}})}\left(1-\frac{w(x_{m+1})}{\sum\nolimits_{j=1}^{m+1}w({x_{j}})}\right)=\frac{w(x_{i})}{\sum\nolimits_{j=1}^{m+1}w({x_{j}})} \] 这个概率仍然满足加权概率的要求。

Reservoir的合并

假如我们现在有两个Reservoir，其中\(A\)已经处理了\(N\)个样本，\(B\)处理了\(M\)个样本，我们可以将这两个Reservoir进行合并，得到一个处理了\(N+M\)样本的大Reservoir。

选择\(A\)的概率: \(w_{sum}^{A}/(w_{sum}^{A}+w_{sum}^{B})\) 选择\(B\)的概率: \(w_{sum}^{B}/(w_{sum}^{A}+w_{sum}^{B})\) 选择\(A\)中样本\(x^{A}_{i}\)的概率 \[ \frac{w_{i}^{A}}{w^{A}_{sum}}\cdot\frac{w_{sum}^{A}}{(w_{sum}^{A}+w_{sum}^{B})}=\frac{w_{i}^{A}}{(w_{sum}^{A}+w_{sum}^{B})} \] 选择\(B\)中样本\(x^{B}_{i}\)的概率

\[ \frac{w_{i}^{B}}{w^{B}_{sum}}\cdot\left(1-\frac{w_{sum}^{A}}{(w_{sum}^{A}+w_{sum}^{B})}\right)=\frac{w_{i}^{B}}{(w_{sum}^{A}+w_{sum}^{B})} \]

仍然符合加权概率的要求。

WRS的好处

采样加权的离散值时，不需要进行预处理以及额外的存储
不关心样本总数
灵活的采样时机，比如在空间上、在时间上或者是多线程上进行采样
具有层次结构，可以分而治之的进行采样

在RIS中使用WRS进行采样

有了RIS和WRS之后，可以将两者结合，每一次生成一个RIS的样本池中的样本后，直接计算权重利用Reservoir进行采样，省去了预处理的以及查找采样的步骤

ReSTIR算法除了将RIS和MRS结合起来以外，还引入了空间(Spatio)和时间(Temporal)上的样本的重复利用。在空间上，ReSTIR会combine当前像素点和邻居像素的reservoirs。在时间上，ReSTIR会存储上一帧的每一个像素的reservoir，和当前帧对应像素的reservoir进行combine。

使用spatialtemporal reuse的原因是因为在通常情况下，近邻像素的几何材质等相关信息和该像素具有相似性，并且在大多数情况下，上一帧的信息也可以在下一帧上进行利用。通过这样的方式，可以扩大合理的样本量，从而进一步降低方差。以下是ReSTIR完整的伪代码。

一些疑问

首先注意到，如果我们使用了邻居像素的reservoir进行合并，但是很明显邻居像素的target PDF和当前像素的显然是不一致的。这里应该如何理解呢？这是因为这里只是将邻居像素的SIR PDF作为了一个新的proposal PDF引入了，实际拟合的target PDF仍然是当前像素的概率分布，所以并不会造成问题。

另一方面，在将RIS和MIS结合起来的时候，MIS的权重选择也是一个问题。通常情况下，MIS的权重采用的是heuristic weights，但是在这里由于无法很方便的计算一个给定方向上的SIR PDF，所以无法实现。因此，论文中采用了uniform的权重，仍然满足MIS的条件。