扩散模型(Diffusion Model)原理详解

发表于 2025-02-19 分类于 ComputerVision 阅读次数：本文字数： 12k 阅读时长 ≈ 11 分钟

Diffusion Model的基本原理(DDPM)

Denoising Diffusion Probabilistic Models(DDPM)在流程上分为两个步骤 - Forward (diffusion) process: 在输入的数据上逐步的增加噪声 - Backward (denoising) process: 在噪声图上进行降噪，从噪声中恢复出原来的图像

Diffusion Process

Diffusion Process是在原始数据的基础上逐步增加噪声，通过超参数迭代次数$T$和variance schedule $\beta_{t} \in (0,1)$ 控制。因此，有以下条件概率 \[ q(\mathbf{x}_{t}| \mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_{t} | \sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t} \mathbf{I}) \] 其中variance schedule满足 \[ 0 < \beta_{1} < \beta_{2} < \cdots < \beta_{T} < 1 \] 这里采样时候需要采用Reparameterization Trick，因为采样是无法进行反向传播的。所以引入一个新的变量$\epsilon$将随机性和传播过程分离开 \[ \begin{align*} \mathcal{N}(\mu,\sigma^{2})&= \mu+\sigma \cdot \epsilon\\ \epsilon &\sim \mathcal{N}(0, \mathbf{I}) \end{align*} \] 所以，diffusion每一步增加噪声可以按照如下操作 \[ \mathbf{x}_{t}=\sqrt{1-\beta_{t}} \mathbf{x}_{t-1} + \sqrt{\beta_{t}} \epsilon \] 由于diffusion process是确定的，在实际过程中并不需要进行每一步迭代，可以直接计算出从原始数据到迭代$T$步后的结果

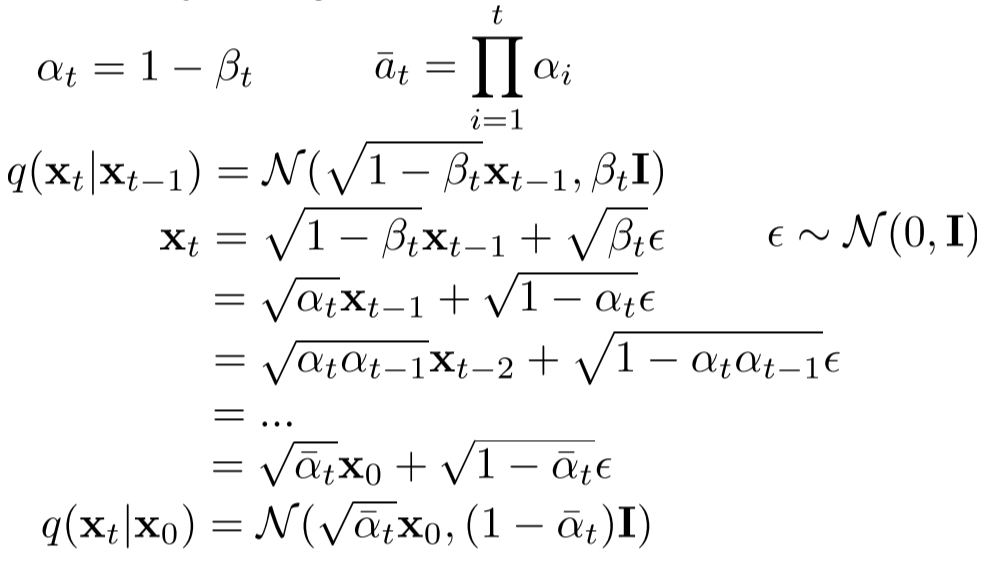
从上面的条件概率中，可以得到diffusion process的closed form \[ \begin{align*} \mathbf{x}_{t} &= \sqrt{\bar{\alpha_{t}}}\mathbf{x}_{0} + \sqrt{1-\bar{\alpha}_{t}} \epsilon\\ \alpha_{t} &= 1-\beta_{t}\\ \bar{\alpha}_{t} &= \prod_{i=1}^{t} \alpha_{i}\\ \epsilon &\sim \mathcal{N}(0, \mathbf{I}) \end{align*} \]

Denoise Process

Denoise process是从噪声图中移除噪声来恢复原图。这个过程需要我们知道概率分布$q(\mathbf{x}_{t-1} | \mathbf{x}_{t})$，也就是从某一时刻的数据反推上一时刻的数据，进行多次迭代后恢复最初的数据$\mathbf{x}_{0}$。根据Bayes Rule， \[ q(\mathbf{x}_{t-1}|\mathbf{x}_{t})=q(\mathbf{x}_{t}|\mathbf{x}_{t-1})\frac{q(\mathbf{x}_{t-1})}{q(\mathbf{x}_{t})} \] 其中 $q(\mathbf{x}_{t})=\int q(\mathbf{x}_{t} | \mathbf{x}_{0}) q(\mathbf{x}_{0}) \mathrm{d} \mathbf{x}_{0}$，但是这一项积分是无法计算的。因此，DDPM采用了神经网络去学习一个模型 $p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})$ 近似估计$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})$。通过推导，可以得到 $q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})$ 也是一个高斯分布，并且高斯分布的均值和方差如下 \[ \begin{align*} \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})\boldsymbol{x}_t + \sqrt{\bar{\alpha}_{t-1}}(1 - \alpha_t)\boldsymbol{x}_0}{1 - \bar{\alpha}_t} \\ \sigma_q^2 &= \frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \end{align*} \] 更进一步的将 $x_0 = \frac{1}{\sqrt{a_t}} \left( x_t - \sqrt{1 - \bar{a}_t} \epsilon \right)$ 带入，可以得到 \[ \mu_q(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t} \sqrt{\alpha_t}} \epsilon \] 个人对为什么用$p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})$拟合$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})$的理解是，当有原始数据和最终的噪声结果的时候，降噪过程是可以计算得到的。但是inference的过程中我们显然是不知道原始数据的，所以希望通过神经网络从原始数据中学习一个采样分布近似的拟合。具体的，给定加噪后的结果$x_{t}$和时间步长$t$，用网络预测从$x_{0}$到$x_{t}$过程中添加的噪声$\epsilon(x_{t}, t)$，预测噪声同时也等价于预测原始图像$x_{0}$，有了$x_{0}$就可以用$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})$进行采样。 \[ p_{\theta}(x_{t-1} | x_{t}) = \mathcal{N}(x_{t-1}; \mu_{\theta}(x_{t}, t), \sigma_t I) \approx q(x_{t-1} | x_{t}, x_0) \]

Training Process

DDPM的损失函数类似于VAE，使用了ELBO的方法，完整推导参见Understanding Diffusion Models: A Unified Perspective

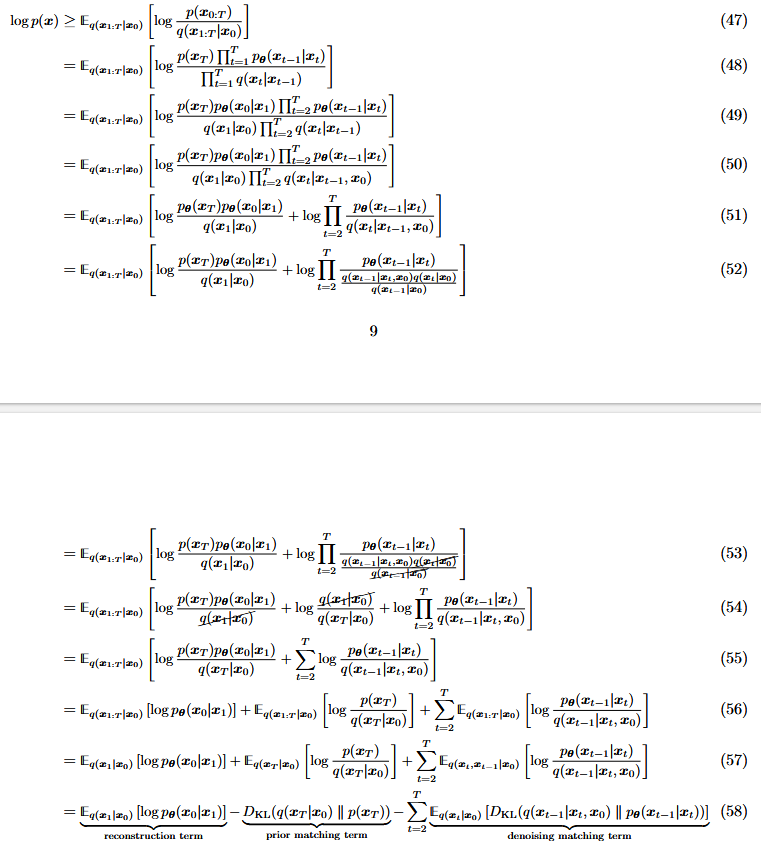
\[ \begin{align*} \log p(\boldsymbol{x}) \geq& \mathbb{E}_q(\boldsymbol{x}_{1:T} | \boldsymbol{x}_0) \left[ \log \frac{p(\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} | \boldsymbol{x}_0)} \right] \\ =&\underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right]}_{\text {reconstruction term }}-\underbrace{D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \| p\left(\boldsymbol{x}_T\right)\right)}_{\text {prior matching term }}\\ &-\sum_{t=2}^T \underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}\left[D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\right)\right]}_{\text {denoising matching term }} \end{align*} \]

Reconstruction term: $\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right]$
Prior matching term: $D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \| p\left(\boldsymbol{x}_T\right)\right)$
Denoising matching term: $\mathbb{E}_{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}\left[D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\right)\right]$

注意到这里reconstruction term和prior matching term实际上就是VAE loss，由于这两项是在diffusion process中没有任何网络参数参与，所以可以看作是常数忽略不计。

由于$q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)$和$p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)$ 都是高斯分布，所以denoising matching term可以实际上转化为 \[ \arg \min_{\theta} D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_\theta(x_{t-1}|x_t)) = \arg \min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \| \mu_\theta - \mu_q \|_2^2 \right] \] $\mu_{q}$在之前已经推导过了，同样的我们可以把模型预测的高斯参数$\mu_{\theta}$写作 \[ \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t} \sqrt{\alpha_t}} \hat\epsilon(x_{t},t) \] 其中$\hat \epsilon(x_{t},t)$是模型预测的噪声，因此最终的损失函数就变成了匹配随机生成的噪声和模型预测的噪声$\|\epsilon-\epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon,t)\|$。

Network Architecture

Diffusion Model目前常见的网络结构主要采用了U-Net + Attention的结构

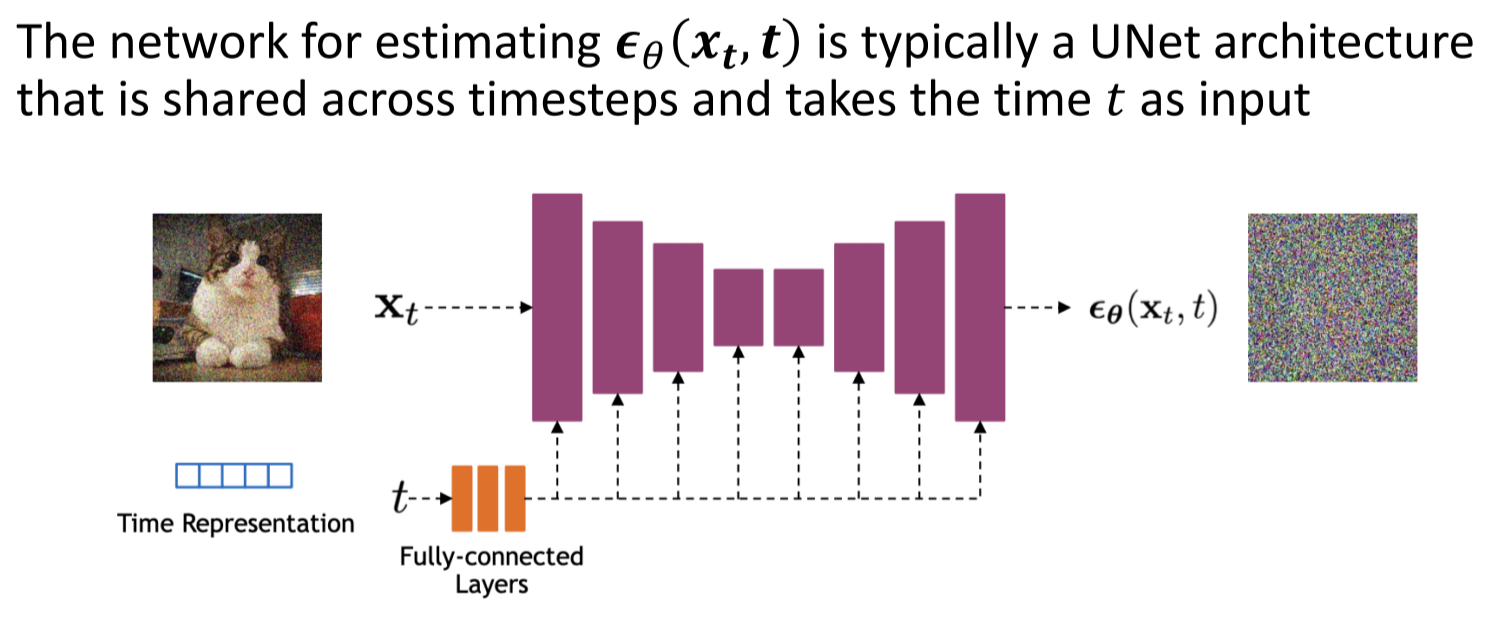
Denosing Diffusion Implicit Model (DDIM)

DDPM存在的一个问题是需要设置比较长的扩散步长才能得到比较好的生成结果，因此生成的速度比较慢。DDIM通过解除DDPM中扩散过程的马尔可夫链的限制，用非马尔可夫过程进行生成，大大提高了DDPM的生成效率。

DDIM注意到了DDPM中的一个问题，就是噪声生成的过程$q(x_{t} | x_{0})$实际上只用了marginal distribution并没有用到join distribution $q(x_{1:T}|x_{0})$，也就是给定$x_0$和时间$t$，加噪的过程实际上是确定的 \[ q(\mathbf{x}_{t} | \mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t}; \sqrt{\alpha_{t}}\mathbf{x_{0}}, (1-\alpha_{t}) \mathbf{I}) \] 因此，如果可以在将马尔科夫链限制去除的同时，能够保持$q(x_{t}| x_0)$有着相同的概率分布，也就是对任意时间步长$t$，使得$q(x_{t}| x_{0})$都满足以上的概率分布。DDIM提出了以下采样概率分布 \[ \begin{align*} q_{\sigma}(x_{t-1}|x_t,x_0) = \mathcal{N}\left( \sqrt{\alpha_{t-1}}x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \frac{x_t - \sqrt{\alpha_t}x_0}{\sqrt{1 - \alpha_t}}, \ \sigma_{t}^2I \right). \tag{1} \end{align*} \] 其中这里的符号$\alpha_{t}$就是DDPM中的$\bar \alpha$

待定系数

在DDPM中，根据贝叶斯公式，有以下结论 \[ p(x_{t-1} | x_{t}, x_{0})=\frac{p(x_{t} | x_{t-1}) p(x_{t-1} | x_{0})}{p(x_{t} | x_{0})} \] 其中我们已知 \[ \begin{align*} p(x_{t} | x_{0}) &= \mathcal{N}(\sqrt{\bar \alpha_{t}} x_{0}, (1-\bar \alpha_{t}) \mathbf{I}) \\ x_{t} &= \sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1 - \bar{\alpha_{t}}} \epsilon '', \textbf{ where } \epsilon'' \sim \mathcal{N}(0, \mathbf{I}) \tag{2} \end{align*} \] 类似的，我们可以进行推广，将DDPM中的马尔可夫链限制去除，我们可以将 $t-1$ 和 $t$ 替换为$s, k$ 其中 $s<k$，得到 \[ p(x_{s} | x_{k}, x_{0})=\frac{p(x_{k} | x_{s}) p(x_{s} | x_{0})}{p(x_{k} | x_{0})} \] 这里$p(x_{s}|x_{0}),p(x_{k}|x_{0})$是已知固定的，但是$p(x_{k}|x_{s})$是未知的。如何设定采样分布的形式呢？这里可以使用待定系数法，将$p(x_{s}|x_{k},x_{0})$设定为和未知变量$k,m,\alpha$有关的高斯分布 \[ p(x_{s}| x_{k},x_{0}) \sim \mathcal{N}(k x_{0} + m x_{k}, \sigma^{2} \mathbf{I}) \tag{3} \] 重参数化并带入已知结论(2) \[ \begin{align*} x_{s} &= kx_{0} + m x_{k} + \alpha \epsilon'\\ &= kx_{0} + m \left(\sqrt{\bar \alpha_{k}} x_{0} + \sqrt{1 - \bar{\alpha_{k}}} \epsilon ''\right) + \sigma \epsilon'\\ &= \left(k+m \sqrt{\bar \alpha_{k}}\right)x_{0} + m\sqrt{1-\bar \alpha_{k}} \epsilon'' + \sigma \epsilon' \end{align*} \] 其中$\epsilon' \sim \mathcal{N}(0,\mathbf{I})$，所以这就是两个独立高斯分布 $\epsilon'$ 和 $\epsilon''$ 的和。因此$x_{s}$满足高斯分布 \[ \begin{align*} x_{s} \sim \mathcal{N}\left(\left(k+m \sqrt{\bar \alpha_{k}}\right)x_{0},m^{2}(1-\bar \alpha_{k})+\sigma^{2}\right) \end{align*} \] 重参数化后已知结论进行对比 \[ \begin{align*} x_{s} &= \left(k+m\sqrt{\bar \alpha_{k}}x_{0}\right) + \sqrt{m^{2}(1-\bar \alpha_{k}) + \sigma^{2}} \epsilon \\ x_{s} &= \sqrt{\bar \alpha_{s}} x_{0} + \sqrt{1 - \bar \alpha_{s}} \epsilon'' \end{align*} \] 根据待定系数得出以下两个方程 \[ \begin{align*} k + m \sqrt{\bar \alpha_{k}} &= \sqrt{\bar \alpha_{s}}\\ \sqrt{m^{2}(1-\bar \alpha_{k}) + \sigma^{2}} &= \sqrt{1 - \bar \alpha_{s}} \end{align*} \] 通过两个方程我们可以将$m,k$解出 \[ \begin{align*} m &= \sqrt{\frac{1 - \bar \alpha_{s} - \sigma^{2}}{1 - \bar \alpha_{k}}}\\ k &= \sqrt{\bar \alpha_{s}} - \sqrt{\frac{(1 - \bar \alpha_{s} - \sigma^{2})\bar \alpha_{k}}{1 - \bar \alpha_{k}}} \end{align*} \] 带入到公式(3)中，可以得到 \[ p(x_{s}| x_{k},x_{0}) \sim \mathcal{N}\left(\left(\sqrt{\bar \alpha_{s}} - \sqrt{\frac{(1 - \bar \alpha_{s} - \sigma^{2})\bar \alpha_{k}}{1 - \bar \alpha_{k}}}\right) x_{0} + \sqrt{\frac{1 - \bar \alpha_{s} - \sigma^{2}}{1 - \bar \alpha_{k}}} x_{k}, \sigma^{2} \mathbf{I}\right) \tag{3} \] 重新整理并让$s=t-1,k=t$时，就可以推出公式(1)

在DDIM的附录中通过数学归纳法证明了，当使用给出的采样概率分布时，是能够满足$q(x_{t}|x_{0})$需要的概率分布的，如下两张图所示

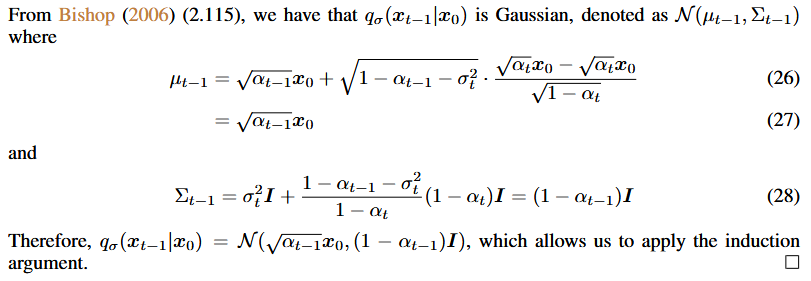
这里利用了结论(2.115)

生成过程

DDIM的生成过程和DDPM是一致的，同样是通过神经网络学习预测噪声，再通过采样分布进行采样进而迭代生成结果。DDIM论文里通过Theorem 1说明了DDIM和DDPM的变分目标是一致的

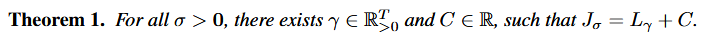
因此可以采用同样的优化目标，也就是对预测的噪声和实际的噪声进行匹配 \[ \begin{align*} L_{\gamma}(\epsilon_\theta) := \sum_{t=1}^T \gamma_t \mathbb{E}_{\\ x_0 \sim q(x_0),\epsilon_t \sim \mathcal{N}({\bf 0}, I) } \left[ \left\| \epsilon_\theta^{(t)}\left( \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon_t \right) - \epsilon_t \right\|_2^2 \right] \end{align*} \] (注：这里开始用的都是DDIM论文中的表示，也就是$\alpha_{t}=\bar \alpha_{t}$) 所以，由于优化目标和生成过程的一致性，DDIM可以利用预训练好的DDPM模型作为优化目标的求解结果，也就是相同的噪声预测网络，只需要调整采样的过程以及参数$\sigma$得到更好的生成过程。

通过将公式(1)进行重参数化展开，以及将$x_{0}$替换为网络预测结果，可以得到以下采样过程 \[ \begin{align*} \boldsymbol{x}_{t-1} = \sqrt{\alpha_{t-1}} \underbrace{\left( \frac{\boldsymbol{x}_t - \sqrt{1 - \alpha_t} \epsilon^{(t)}_{\theta}(\boldsymbol{x}_t)}{\sqrt{\alpha_t}} \right)}_{\text{"predicted $\boldsymbol{x}_0$"}} + \underbrace{\sqrt{1 - \alpha_{t-1} - \sigma^2_t \cdot \epsilon^{(t)}_{\theta}(\boldsymbol{x}_t)}}_{\text{"direction pointing to $\boldsymbol{x}_t$"}} + \underbrace{\sigma_t \epsilon_t}_{\text{random noise}} \end{align*} \] 其中，当$\sigma_t = \sqrt{\frac{1 - \alpha_{t-1}}{1 - \alpha_t}} \sqrt{1 - \frac{\alpha_t}{\alpha_{t-1}}}$时，生成过程等价于DDPM；而当$\sigma_{t}=0$时，这时random noise就是0，所以生成过程就失去了随机性变成了一个确定的过程，论文中将这种情况称之为denoising diffusion implicit model (DDIM)

$\sigma_{t}$可以写成是$\eta (\sqrt{\frac{1 - \alpha_{t-1}}{1 - \alpha_t}} \sqrt{1 - \frac{\alpha_t}{\alpha_{t-1}}})$的形式，其中$0 \leq \eta \leq 1$用于控制生成过程

加速生成模型

DDIM论文提出了这样一个观点：DDPM的训练结果实质上包含了它的任意子序列参数的训练结果。因此，生成过程不需要严格遵循$(x_{T}, \cdots, x_{1})$的过程，而是可以进行跳跃步，选择其中的一个长度为$S$的子序列$(x_{\tau_{S}},\cdots,x_{\tau_{1}})$做生成，只需要满足 \[ q(x_{\tau_{i}} | x_{0}) = \mathcal{N}(x_{\tau_{i}};\sqrt{\alpha_{\tau_{i}}x_{0}}, (1- \alpha_{\tau_{i}}) \mathbf{I}) \] 如下图所示，本来生成过程是$x_{3} \rightarrow x_{2} \rightarrow x_{1} \rightarrow x_{0}$ ，现在可以跳步，变成了$x_{3} \rightarrow x_{1} \rightarrow x_{0}$

📌方差选择整理(DDPM & DDIM)

DDPM 的方差选择1：

$\sigma_{t, \theta}^2 = \Sigma_{\theta}(x_t, t)$
- 模型学习的方差（称为 learned）
- 实际未在 DDPM 中使用，但被 GLIDE 采用。
$\sigma_{t, s}^2 = \beta_t = \frac{1 - \alpha_{t-1}}{1 - \alpha_t} \beta_t$
- 由公式 (8-1) 推导得出（称为 fixedsmall）
- 用于 celebahq 和 lsun 数据集。
$\sigma_{t, l}^2 = \beta_t$
- 称为 fixedlarge，用于 cifar10 数据集
- 满足 $\sigma_{t,l} > \sigma_{t,s}$，即方差更大。

DDIM 的方差选择： - $\sigma_t(\eta)^2 = \eta \cdot \hat{\beta}_t$
- 基于 DDPM 的 fixedsmall 版本，额外乘以系数 $\eta$。

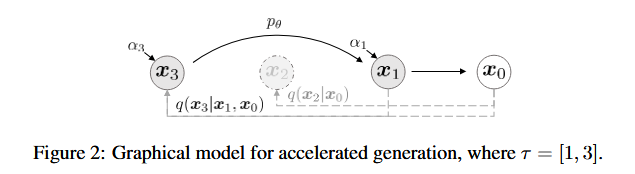
Latent Diffusion Model (Stable Diffusion)

DDPM还存在一个问题，就是需要大量的计算资源。由于DDPM直接在图像空间上进行训练和推理，导致了非常耗时。LDM (Latent Diffusion Model)也就是Stable Diffusion提出了一种方法，首先将图像用VAE encode为一个低分辨率的latent space，在latent space上进行生成，然后再将latent space decode还原为图像空间，能够大大降低训练推理所需的计算资源。

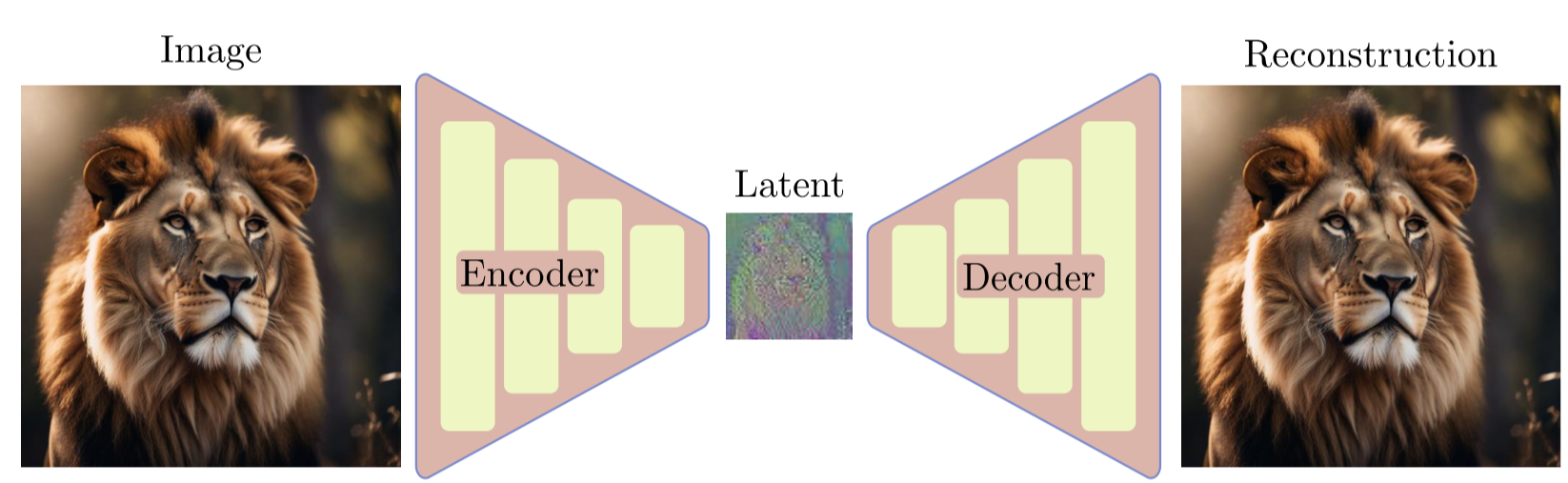
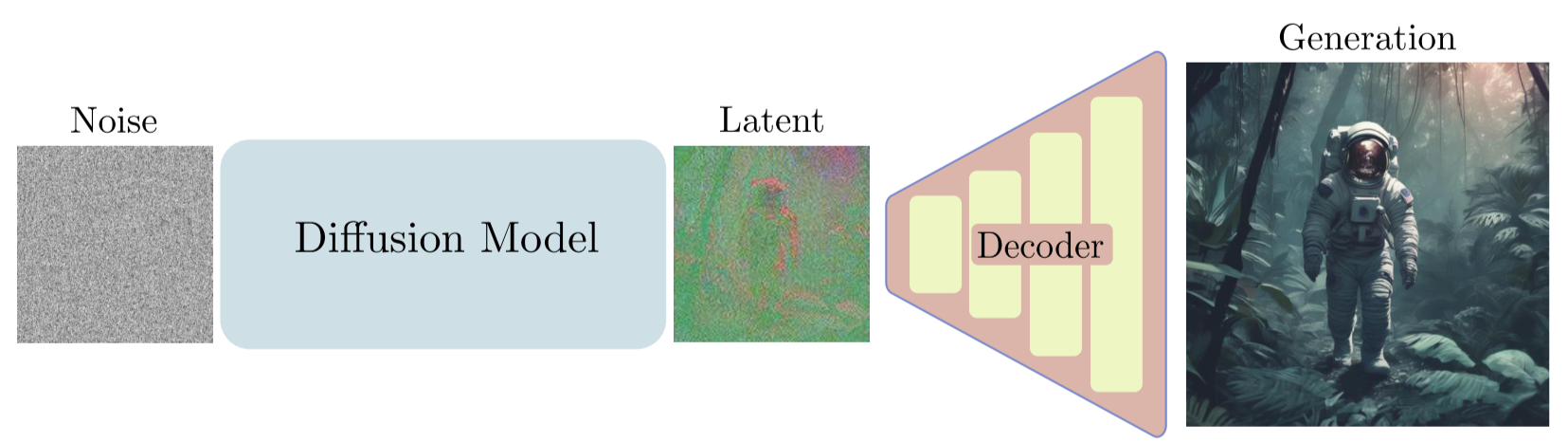
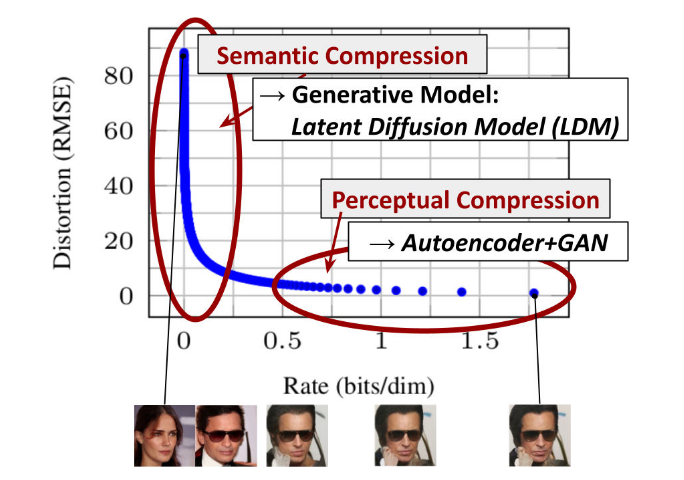
LDM论文观察到，DDPM模型对图像的压缩通常由perceptual compression和semantic compression组成。因此，LDM提出可以用Autoencoder将图像的perceptual information在训练中剔除掉，只让Diffusion Model对semantic的部分压缩。

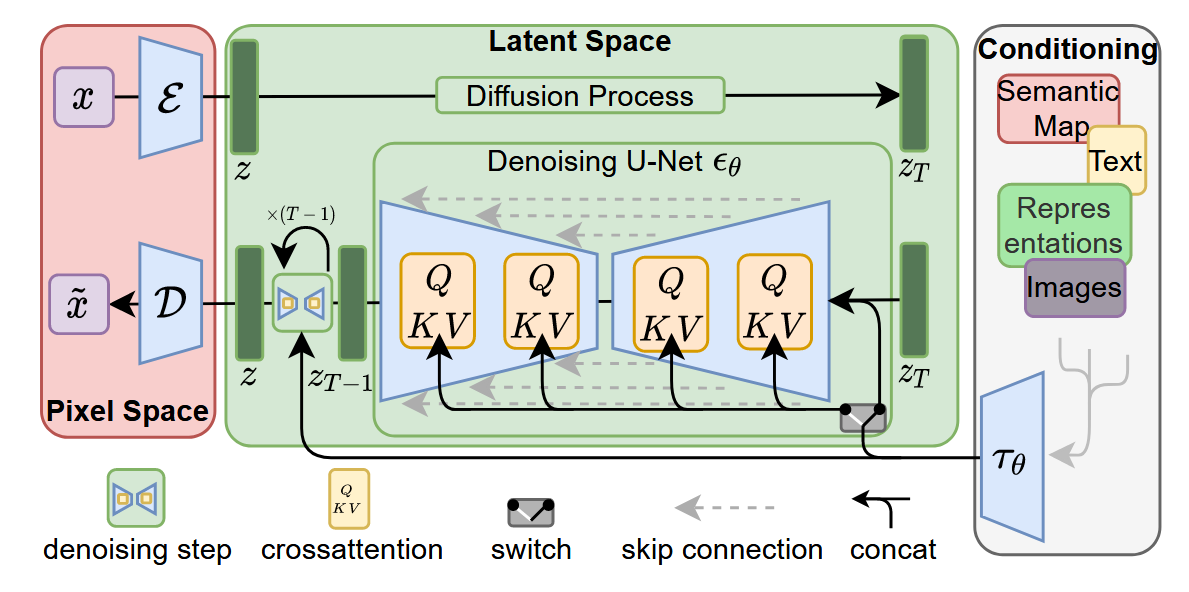
LDM采用的网络架构如下图所示，其中$\varepsilon$ 和$\mathcal{D}$分别是预训练好的Autoencoder中的Encoder和Decoder。通过Encoder首先将图片进行perceptual compression得到latent space $z$，然后在latent space通过diffution process进行加噪。Denoise process采用了带有Attention的UNet架构，通过Cross Attention注入conditioning信息。

Attention由很多变种，在LDM中主要有Self Attention和Cross Attention两种。

Cross Attention
- $CrossAttn(A,B)=Attentino(W_{Q} \cdot A, W_{K} \cdot B, W_{V} \cdot B)$
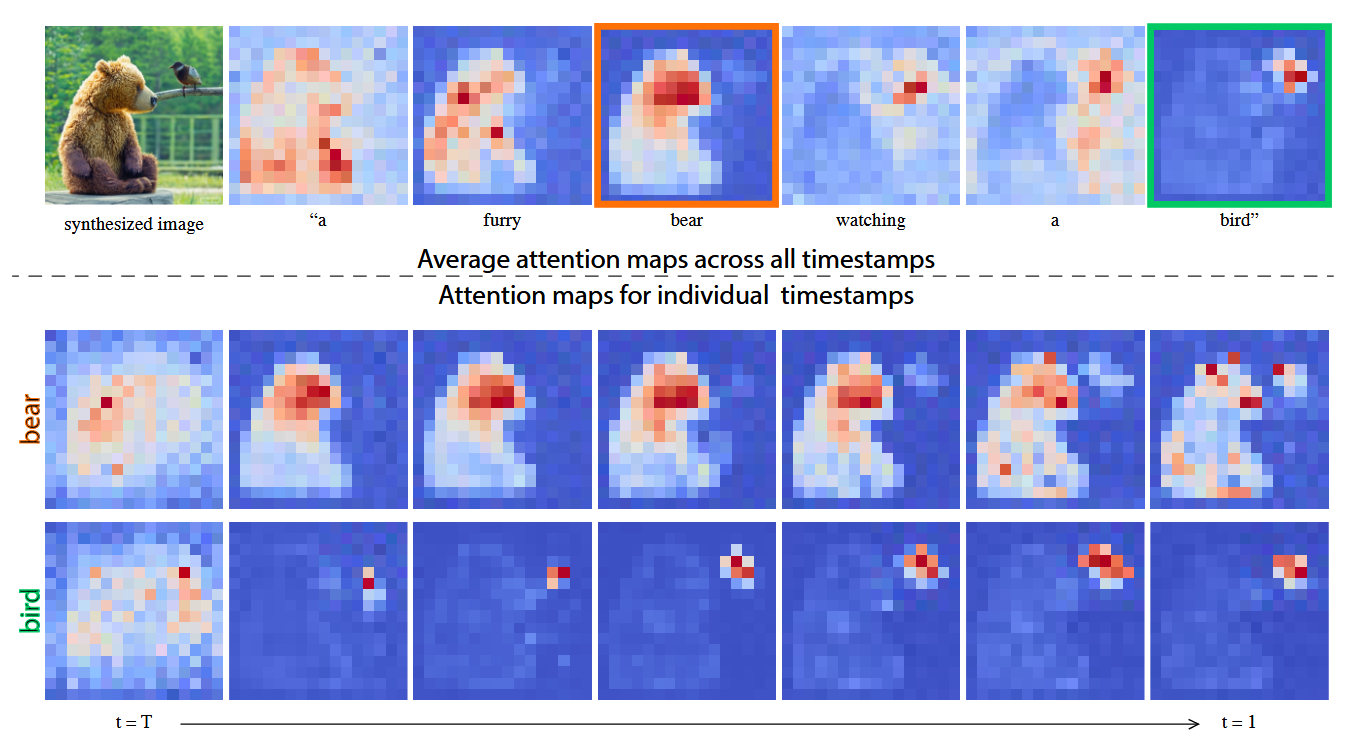
- 可以理解为利用A对B上的信息进行Query，比如在下图中，不同的文本token会产生不同的attention map
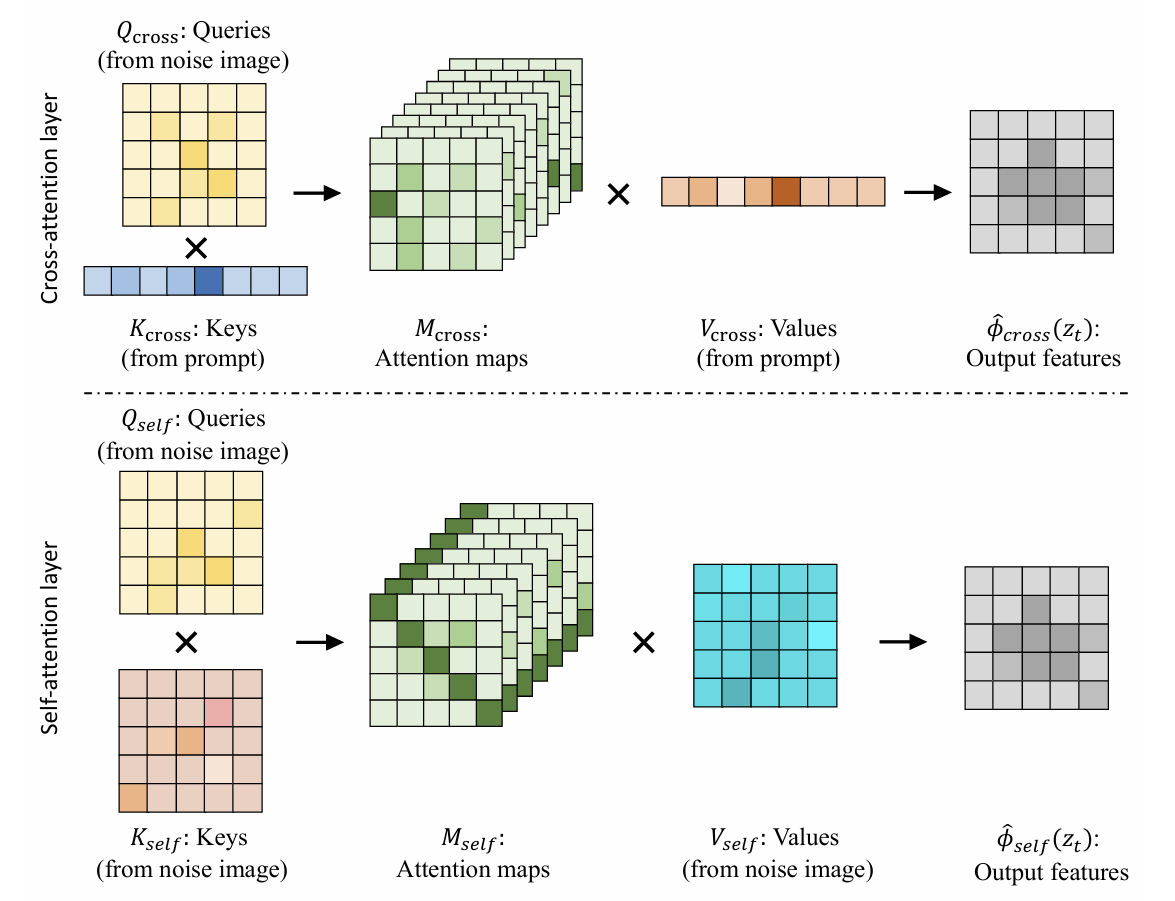
Self Attention
- $SelfAttn(A)=Attention(W_{Q} \cdot A, W_{K} \cdot A, W_{V} \cdot A)$
- 可以理解为A自己作了一次特征提取，将重要的信息提取出来

总结一下，LDM最主要的是两个贡献

在diffusion model的基础上，对图像空间进行压缩，在压缩后的latent space上进行diffusion生成
使用cross attention将conditioning信息注入到网络中